- #1
Tzabcan
- 10
- 0
So, I have the matrix:
A = -1 -3
3 9
Eigenvalues i calculated to be λ = 8 and 0
Now when i calculate the Eigenvector for λ = 8, i get the answer -1
3
Then when solve for the eigenvector for λ= 0 I get the eigenvector 3
-1
Both incorrect, they're supposed to have the signs the opposite way round. I don't understand how I am getting it wrong.
This is how i am attemption to solve it.
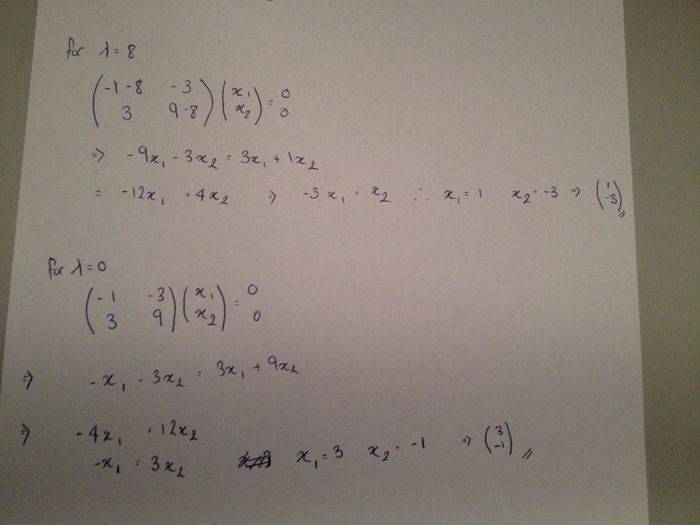
Any pointers would be appreciated.
A = -1 -3
3 9
Eigenvalues i calculated to be λ = 8 and 0
Now when i calculate the Eigenvector for λ = 8, i get the answer -1
3
Then when solve for the eigenvector for λ= 0 I get the eigenvector 3
-1
Both incorrect, they're supposed to have the signs the opposite way round. I don't understand how I am getting it wrong.
This is how i am attemption to solve it.
Any pointers would be appreciated.