Energy conservation of a light spring

[haha1234]

Homework Statement

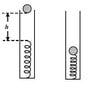
A light spring is fixed to the bottom of a vertical tube.A ball is released from rest at a height h above the upper end of the spring as shown.After rebounding several times the ball eventually comes to rest and stay on top of the spring.Assume all contact surfaces are smooth and the spring obeys Hooke's law throughout.Which of the following statement is/are true?

(1)The compression of the spring is proportional to the mass of the ball.
(2)The compression of the spring is independent of the height h.
(3)The gravitational potential energy lost by the ball is equal to the strain energy stored in the spring.

Homework Equations

The Attempt at a Solution

The question state that the contact surface is smooth so energy cannot lose because of friction.So why the the ball eventually stop as the energy in the system is conserve?
And I would like to know why (2) is correct.The value of h determine the gravitational potential energy before releasing the ball,so the maximum potential energy stored in the spring depends on h.

 

[adjacent]

Your have not posted the image.Please re upload.

 

[haha1234]

Your have not posted the image.Please re upload.

Uploaded.

 

[ehild]

Some of the energy is dissipated inside the spring, because of internal friction. As the spring compresses and releases, its particles move with respect to each other and their motion transforms to internal energy (heat).

ehild

 

[haha1234]

Some of the energy is dissipated inside the spring, because of internal friction. As the spring compresses and releases, its particles move with respect to each other and their motion transforms to internal energy (heat).

ehild

Thanks.
And I would like to ask why the compression of the spring is independent of the height h.
As 1/2kx²=mgh,the compression of the spring depends on h.

 

[ehild]

But energy is lost. The ball is in rest on the top of the spring, in equilibrium, and it "forgot" from what height it had fallen down initially. The opposite forces, gravity and spring force balance each other: mg=kx.

ehild