- #1
alco19357
- 18
- 0
Homework Statement
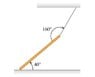
A uniform, 210-kg beam is supported by a cable connected to the ceiling, as shown in the figure . The lower end of the beam rests on the floor.
a. What is the tension in the cable?
b. What is the minimum coefficient of static friction between the beam and the floor required for the beam to remain in this position?
Homework Equations
[itex]\Sigma[/itex]F_x = 0
[itex]\Sigma[/itex]F_y = 0
[itex]\Sigma[/itex]Torque = 0
The Attempt at a Solution
So we draw a free body diagram for both the beam and cable. I have 4 forces (perhaps I'm wrong with how many forces I actually have)
I have a normal x and y force on the ground acting on the beam.
I have gravity acting on the beam. I have tension acting on the beam. And that's all I believe.
So I get N_x + Tcos40 = F_x
and... N_y + Tsin40 = F_y
and... Torque = T*cos160*r - mgcos40 << the length of the beam isn't given though?
Please help