- #1
leroyjenkens
- 616
- 49
Homework Statement
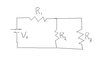
Write an expression for the voltage across R3 in terms of V0, R1, R2, and R3. Under what condition is the voltage across R3 approximately independent of the value of R3?
Homework Equations
I uploaded a picture.
I think Req = R1 + R2...
and 1/Req = 1/R1 + 1/R2...
Are what I need.
The Attempt at a Solution
Best thing I could think of doing was adding R2 and R3, and then add R1 to get this:
1/R2+R3 + R1, but I don't know how to include the voltage.
And I have no idea what it means by what condition is the voltage across R3 approximately independent of the value of R3.