- #1
Dustinsfl
- 2,281
- 5
How do I find the first 10 positive solutions numerically?
$$
\tan x = \frac{1}{x}
$$
$$
\tan x = \frac{1}{x}
$$
Dustinsfl said:How do I find the first 10 positive solutions numerically?
$$
\tan x = \frac{1}{x}
$$
Where are you stuck?Dustinsfl said:How do I find the first 10 positive solutions numerically?
$$
\tan x = \frac{1}{x}
$$
Ray Vickson said:How do you find the first positive solution? You tell US; do not ask us to tell you: read the forum rules.
RGV
SammyS said:Where are you stuck?
What have you tried?
After 490 posts, you should know the drill here at PF .
But here's one hint: One thing I would try is to take the reciprocal of both sides of that equation, giving you:[itex]\displaystyle \cot(x)=x[/itex]
Graph each side.
dextercioby said:Numerically means approximately since this is a transcendental equation. Only some computer software would give you the results, I think.
http://www.wolframalpha.com/input/?i=Plot+y(x)+=+tan+x+-+1/x
Dustinsfl said:I am not good at numerical analysis. I haven't taken a course in it yet as well as in Matlab. I will be taking Matlab this spring and Numerical Analysis next fall. So when I know how to do it and use Matlab efficiently, I won't even ask you.
SammyS said:Here are the graphs of y=x and y=cot(x), superimposed. (from WolframAlpha)
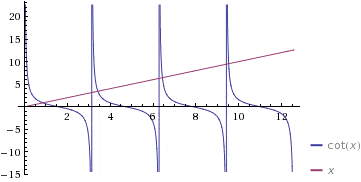
Dustinsfl said:I tried using NSolve in Mathematica but that didn't work.
I also tried
syms x
solve(tan(x)==1/x)
in Matlab and that just gave -263.
How can I do this in one of these programs?
This is what I wrote in post 3.
I can make graphs of this with the Tikz package and in Mathematica (that isn't the challenge here). How can I use Mathematica or Matlab to generate the first 10 positive solution?
Thanks. Hopefully in the spring when I take programming in Matlab I will be better at this.Ray Vickson said:I don't have access to Mathematica (except through Wolfram Alpha) or to Matlab, but in Maple it is easy:
S:=fsolve(tan(x)=1/x,x=0..Pi/2),seq(fsolve(tan(x)=1/x,x=Pi/2+(i-1)*Pi..Pi/2+i*Pi),i=1..9);
S := 0.8603335890, 3.425618459, 6.437298179, 9.529334405,
12.64528722, 15.77128487, 18.90240996, 22.03649673,
25.17244633, 28.30964285
I'm sure it must be possible, even easy, to do the same thing in Mathematica.
RGV
Try using FindRoot instead.Dustinsfl said:I tried using NSolve in Mathematica but that didn't work.
Dustinsfl said:I tried using NSolve in Mathematica but that didn't work.
...
How can I do this in one of these programs?
The tangent function, or Tan x, is a mathematical function that represents the ratio of the opposite side to the adjacent side of a right triangle.
The domain of this equation is all real numbers except for 0, as division by 0 is undefined.
This equation can be solved using algebraic manipulation and the properties of trigonometric functions. One approach is to rewrite the equation as sin x = cos x / x and then use the Pythagorean identity to simplify further.
Yes, there is a specific value of x where this equation holds true. It is approximately 0.8603, which can be found using a graphing calculator or by solving the equation using trigonometric identities.
The relationship between Tan x and 1/x is that they are reciprocals of each other. This means that if one value is plugged into the equation, the other value will be the reciprocal of that number. For example, if Tan x = 2, then 1/x = 1/2.