Finding the Locus of the Mid-Point of a Ladder Against a Vertical Wall

[BrendanM]

After working hours on my first assignment LOL (i really want to do good in school) i hav ebecame stumpted.
The question is:
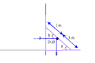
A ladder, 2 meters long, is standing flat against a vertical wall. The foot of the ladder is pulled away from the wall. As this happens, the top of the ladder stays in contact with the wall. The process stops when all of the ladder is on the ground. What is the locus of the mid-point of the ladder? (I.e., give a function which describes what happens to the mid-point of the ladder.) I am not sure how to approach this problem so I am posting here, I am going to work on it for a while then go to bed. If someone could help me out that would be great. thanks u

 

[BrendanM]

damn I am rusty, i thnk i got it... y= sqr(2^2 -x^2)/2 correct me if I am wrong

 

[BrendanM]

nm I am wrong

 

[Leong]

Hang on for 10 minutes. Hints are coming soon.

 

[BrendanM]

cool ill stay up for a bit, I am still working on it !

 

[Leong]

Upper triangle :
$$x= cos \theta$$
Lower triangle:
$$y = sin \theta$$
Use trigo identity.

 

[BrendanM]

hmm ill think about this for a minute, thanks for help. hmm what do you mean by use trig identity

 

[Leong]

$$sin^2\theta + cos^2\theta=1$$
This will be the answer actually.

 

[BrendanM]

wouldn't the answer be y = sqr(1-cos^2(x))

im really really sick right now... so I am going to bed, ill check this out in the morning, i hope i am well for school :| thanks

 

[Leong]

No. the answer is $$x^2+y^2 =1$$

 

[Sabine]

yes dats ryt its a cercle (r= 1m)

 

[HallsofIvy]

Set up your coordinate system so that the wall of the house is the positive y-axis and the ground is the positive x axis. The coordinates of the upper end of the ladder are (0, Y) and the coordinates of the lower end are (X,0) where X²+ Y²= 2. The midpoint of the ladder is at (X/2, Y/2). Letting x= X/2, X= 2x so
X²= 4x² and let y= Y/2 so Y= 2x and Y²= 4y². Then X²+ Y²= 4x²+ 4y²= 2 so the locus of the midpoint is given by x²+ y²= (1/2) (x and y both non-negative). That is,a the midpoint moves on a circle (actually the portion in the first quadrant) with center (0,0) and radius $\frac{\sqrt{2}}{2}$.

 

[mathwonk]

i guess halls of ivy meant X^2 + Y^2 = 4?