- #1
Tclack
- 37
- 0
I can do vertically submerged fluid force problems. One portion of my book says:
If a flat surface is immersed so that it makes an angle of [itex]0 \leq \theta \geq \frac{\pi}{2}[/itex] with the vertical, then the fluid force on the surface is given by:
[itex]F=\int^b_a \rho h(x)w(x)sec\theta dx[/itex]
Can someone explain exactly what the sec(theta) is giving me; how exactly this equation changing the original equation of a vertically submerged surface. I never took trig., so please dumb it down in that area
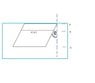
If it helps, just made a diagram. Is this the correct angle in the equation?
If a flat surface is immersed so that it makes an angle of [itex]0 \leq \theta \geq \frac{\pi}{2}[/itex] with the vertical, then the fluid force on the surface is given by:
[itex]F=\int^b_a \rho h(x)w(x)sec\theta dx[/itex]
Can someone explain exactly what the sec(theta) is giving me; how exactly this equation changing the original equation of a vertically submerged surface. I never took trig., so please dumb it down in that area
If it helps, just made a diagram. Is this the correct angle in the equation?