Gradient equal to multiplying by vector?

[Isaac0427]

Hi guys!
So I have been researching the electric field, and I have come upon some interesting equations that confused me a little (all from wikipedia):

,

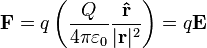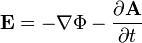, and

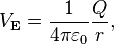with V being the same as psi. Doing the algebra, I would get (Q/4πε₀)*(r-hat/|r|²)=-∇(Q/4πε₀r)-∂A/∂t. Now in the case that A does not change with time, we would get that taking the negative gradient is equal to multiplying by r-hat/|r|. Is this correct?

 

[MisterX]

Yes, this is true for the gradient of $\frac{1}{|r|}$. $$-\nabla \frac{1}{|r|} = \frac{\hat{\mathbf{r}}}{|r|^2}, \;\;\;\;\;\;\;\;r\neq0.$$

 

[Isaac0427]

Yes, this is true for the gradient of 1|r|\frac{1}{|r|}.

Would the negative gradient of 2|r|\frac{2}{|r|} be 2r-hat over |r|²?

 

[Isaac0427]

Would the negative gradient of 2|r|\frac{2}{|r|} be 2r-hat over |r|²?

Sorry, I don't know what happened with the code. I was asking bout 2/|r|

 

[lightarrow]

Would the negative gradient of 2|r|\frac{2}{|r|} be 2r-hat over |r|²?

you can always take a moltiplicative constant out of the gradient.

--
lightarrow