Help with Integral Time (Ti) and Derivative Time (Td)

[BoilingHeat]

Hello,

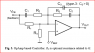
I've been studying PID control and I've undestrood many things, but in every source I've read there is no exact definition for what the Integral Time and Derivative Time are. I now know what is the results of setting them high and low—to some extent—and have studied a bit the tuning methods for when you don't have a model for the plant. But exactly what is the Ti? If the integral of the error is always being calculated, then what is the exact definition for it? Same for the Td. Thanks in advance.

 

[meBigGuy]

Maybe this will help
http://digital.ni.com/public.nsf/allkb/6E76EC47B831FAED86256E4E007347DC

 

[anorlunda]

've been studying PID control and I've undestrood many things, but in every source I've read there is no exact definition for what the Integral Time and Derivative Time are.

That is something you should have learned in school. It is a bit embarrassing to need to ask that question. But if you don't understand those concepts, then you probably won't the correct answers that meBigGuy provided. Here's a "poor mans" version stated as an algorithm.

1. We start with the controller error $e$. $e$ can be + or -.
2. We will do a repeated calculation every D seconds. Make D as small as you can.
3. The time integral of $e$ (that you call $Ti$) can be computed as $Ti_{now}=e_{now}*D+Ti_{previous}$
4. The time derivative of $e$ (that you call $Td$) can be computed at $Td_{now}=\frac{e_{now}-e_{previous}}{D}$
5. At the end of the calculation, the $now$ values get copied to the $previous$ values.
6. After D seconds pass, GO TO 3

 

[jim hardy]

My thought process is analog, in fact that's my "handle" on other forums...

Another article
http://electronicdesign.com/analog/whats-all-p-i-d-stuff-anyhow

But exactly what is the Ti

It is the time constant of the integrator inside your controller
Thought experiment - though you can actually do this on the bench and it's how we calibrate controllers..
assume a controller with gain of 1.0 and establish a constant error of 1% at its input . That'll make it integrate.
Measure how long it takes the controller's output to change by 1% ? That's a definition of Ti .
Some manufacturers would include gain in that measurement others would not.
That amount of change in output, equal to error(or maybe error X gain), is called a "repeat" as in 'repeating' the error.
Some manufacturers call Ti "Reset time" , the time required for output to change by one 'repeat' .
You will encounter "Reset Time" given by various manufacturers as either 'minutes per repeat' or 'repeats per minute'. Probably by various textbook authors, too . Don't be intimidated. There's just no standardization.

For me, easiest way to keep it straight is to go back to this circuit diagram
http://www.ecircuitcenter.com/Circuits/op_pid/op_pid.htm

Look at bottom opamp, which is the integrator:
R1C1 is Ti , reset time ( or is that RICI? i can't tell if they used number 1 or letter I .)
and over at rightmost amp R9/R8 is gain.

There are many many circuit arrangements out there.
Nowadays most of them are embedded microcomputers using Anorlunda's algorithm or similar.

 

[BoilingHeat]

This forum is awesome.

That is something you should have learned in school. It is a bit embarrassing to need to ask that question.

Not embarrassing at all actually. Thanks for your reply and let me ask you another surely dumb question, I would appreciate it if you can explain. You call Ti and Td the Time Integral and Time Derivative respectively, but, do you mean Integral and Derivative with respect to time? Or you just inverted the words, because if you mean the time I think it should be "Integral Time" and "Derivative Time".

Now, if you mean the Integral of e with respect to time, then: You're calculating the area with e_now * D, and then adding it to the previous areas already calculated, right? That way you get the accummulation of errors, but I don't see where the definition of the Integral Time is. Could you please explain this? Regarding the Td: You're getting the error with respect to the interval D, I mean, how it is changing every D seconds, that gives a rate of change, but, again, Td is not a rate of change and Ti is not an area, they are seconds. Probably I just misunderstood, if I did please explain.

My thought process is analog, in fact that's my "handle" on other forums...

It is the time constant of the integrator inside your controller

Thanks a lot Jim, I think getting back to OpAmp in this case will give me a better insight. Unfortunately the article is missing the figures. I'll have a look at all this and likely come back with a few questions.

Maybe this will help
http://digital.ni.com/public.nsf/allkb/6E76EC47B831FAED86256E4E007347DC

Thanks meBigGuy, although anorlunda is right and I need to get a grasp on those things first.

 

[jim hardy]

Unfortunately the article is missing the figures.

Ouch that's frustrating !

i use Firefox and Windows 7 , they pop right up for me.
http://www.ecircuitcenter.com/Circuits/op_pid/op_pid.htm

here's a similar pdf link,
http://web.mit.edu/2.010/www/lab/LAB8.PDF
he calls the P element 'gain' instead
but if you like analog circuits it's straightforward.

google returns plenty of articles

 

[jim hardy]

There's a single amplifier implementation dating back to early days of opamps, 1940's

it's derived here in excruciating detail starting at 8:00


i didnt check his algebra , am not sure about his derivative term
but don't know it to be incorrect either

 

[anorlunda]

This forum is awesome.
Not embarrassing at all actually. Thanks for your reply and let me ask you another surely dumb question, I would appreciate it if you can explain. Opp call Ti and Td the Time Integral and Time Derivative respectively, but, do you mean Integral and Derivative with respect to time? Or you just inverted the words, because if you mean the time I think it should be "Integral Time" and "Derivative Time".

Now, if you mean the Integral of e with respect to time, then: You're calculating the area with e_now * D, and then adding it to the previous areas already calculated, right? That way you get the accummulation of errors, but I don't see where the definition of the Integral Time is. Could you please explain this? Regarding the Td: You're getting the error with respect to the interval D, I mean, how it is changing every D seconds, that gives a rate of change, but, again, Td is not a rate of change and Ti is not an area, they are seconds. Probably I just misunderstood, if I did please explain.
Thanks a lot Jim, I think getting back to OpAmp in this case will give me a better insight. Unfortunately the article is missing the figures. I'll have a look at all this and likely come back with a few questions.
Thanks meBigGuy, although anorlunda is right and I need to get a grasp on those things first.

I used the nomenclature Ti and Td only because you used those terms in your original question.

The algorithms were for the integral of e with respect to time, and the derivative of e with respect to time. Those are the correct nomenclature.

 

[BoilingHeat]

Ouch that's frustrating !

i use Firefox and Windows 7 , they pop right up for me.
http://www.ecircuitcenter.com/Circuits/op_pid/op_pid.htm

here's a similar pdf link,
http://web.mit.edu/2.010/www/lab/LAB8.PDF
he calls the P element 'gain' instead
but if you like analog circuits it's straightforward.

google returns plenty of articles

There's a single amplifier implementation dating back to early days of opamps, 1940's

it's derived here in excruciating detail starting at 8:00


i didnt check his algebra , am not sure about his derivative term
but don't know it to be incorrect either

Thank you very much, let me get to those and come back with some more questions.

I used the nomenclature Ti and Td only because you used those terms in your original question.

The algorithms were for the integral of e with respect to time, and the derivative of e with respect to time. Those are the correct nomenclature.

Thank you, but my question was about those two times, not the integral and derivative themselves, those I can understand—although not thoroughly given the problems with the Td and Ti.

 

[meBigGuy]

I may be wrong but I think of the integral time as relating to the time constant of integration and the derivative time as relating to the time constant of derivation.
I think of it as the intervals at which data is sampled to do the integral and derivative.

 

[BoilingHeat]

Measure how long it takes the controller's output to change by 1% ? That's a definition of Ti .

Okay, I went back to the integrator with the OpAmp, and understood your statement. With the OpAmp, RC represents the time it takes the integrator to reach the input value when it's constant (we may consider the difference between the constant input and a 0 value output as the initial error, right?). I thought it was the time it takes the integrator to correct a unity error, but making some calculations it seems that it applies to any magnitude in the input. Please correct me if I'm wrong, I haven't been able to go through all the material, I'm doing it now and through the differentiator to understand the Td. I'll come back with some more questions.

Thanks a lot.

 

[jim hardy]

With the OpAmp, RC represents the time it takes the integrator to reach the input value when it's constant (

I don't quite grasp that statement. You may have tried to convey the right concept I'm not sure.

We calibrate controllers on the bench open loop ie not in a system.
It's down in the dirt simple - we apply step changes and watch output usually on a stripchart recorder so there's a calibration record
To check integral time here's how i might do it
Set proportional to 1.0
set integral to 1 repeat per minute
apply input to create zero error
set output to some convenient value , industrial controllers have a provision for manual control that allows this

transfer from manual control to auto, allowing integral to become active
controller output should hold constant since integrator sees zero error
start a stopwtach and
change input from zero to (?)some convenient amount of error say 10%
output should change immediately by same amount because of proportional term
output should continue changing at uniform rate by 10%(the amount of error) every minute
after a few minutes return error to zero
output should drop by 10%due to proportional , and hold at new value because integrator once again sees 0 error at input.

i have thereby verified that the proportional term is correct, output step was same size as inpuit step
and the integral term is correct, output repeats error once per reset time AND integration is linear
nonlinearity in integration says there's a hardware problem maybe an air leak in pneumatic or an unbalanced opamp in electronic

I thought it was the time it takes the integrator to correct a unity error,

That sound to me like something you could only measure in a closed loop and the remainder of the loop's dynamics would get into the act. We test them open loop because it's so much easier to interpret the result. Any adjustment when the thing is plugged into the plant is for purposes of tuning the process.
For example
<<<< boring anecdote alert>>>
our feedwater controllers ran for twenty years with the same settings.
Engineering decided to increase by 10% the amount of feedwater valve travel
when they did we observed that at low power we got sinewave oscillation in feedwater flow, large enough to make operators uneasy.
AHA! They'd raised loop gain by making that valve move farther
It only caused trouble at low power where valve is barely open and a small movement is a big % of the small flow
a small tweak downward on the proportional dial fixed it immediately.
Plant manager said :" That dog'll hunt, Thanks."
I honestly replied "Thanks for the kind words, but really It was nothing."
Hope that too long dissertation helps

you have to understand controllers open loop, then integrate them into closed loop controlling a process. It's two ways of thinking - just train yourself to separate them

old jim