- #1
cajswn
- 2
- 0
Can someone help with this question, please?

This is what I tried but I don't think it's correct.
Also what does sx = 8.6 and sy = 7.4 represent?
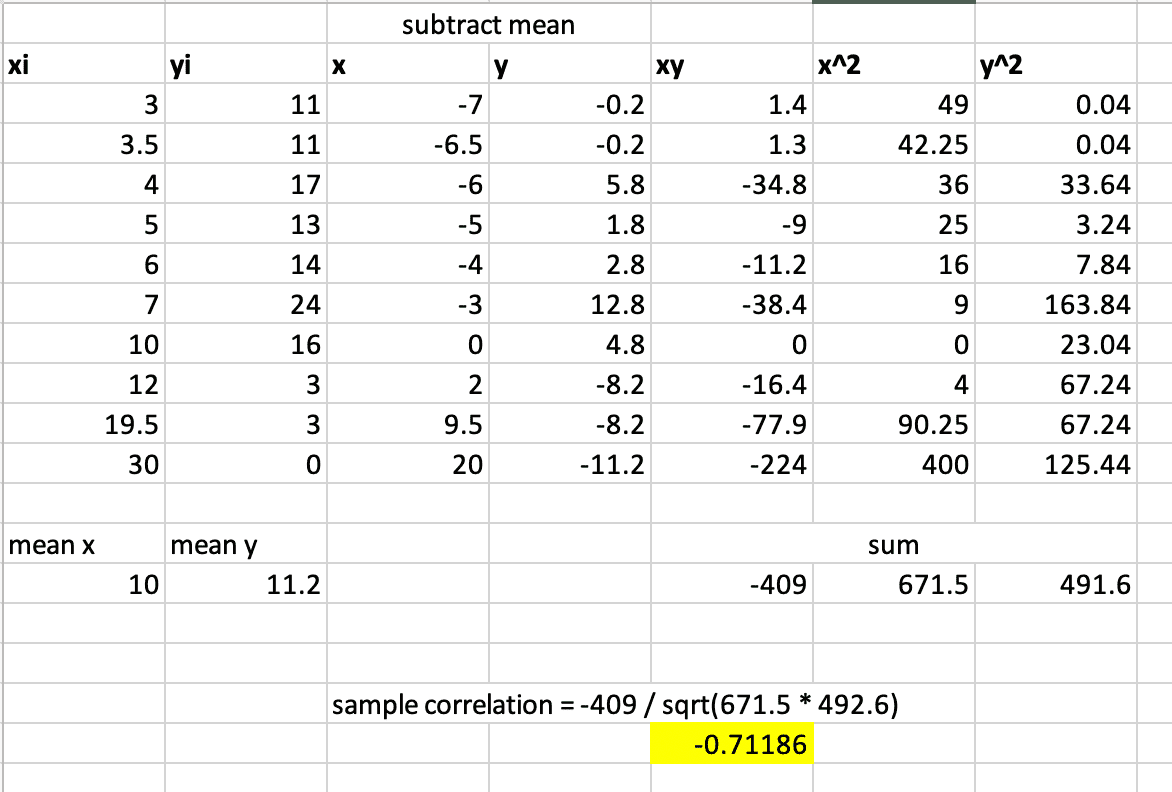
This is what I tried but I don't think it's correct.
Also what does sx = 8.6 and sy = 7.4 represent?