How can the motion of point A be determined in this system?

[Vibhor]

Homework Statement

Homework Equations

The Attempt at a Solution

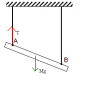
When string joining B is burnt , the forces acting on the rod are its weight , and tension in the left string ,both being vertical ,the acceleration of its COM would be vertical . Hence option A is correct .

Now how should particle at A move ?

Please help me with the problem .

Thanks

 

[Hesch]

Why don't you try it out?
http://www.buero-netshop.de/shop/images/products/main/q-connect-lineal-20cm-kunststoff-transparent.jpg
Hang it ( in the hole, using sewing thread ) and hold it ( at 20cm ). Let it go.

Watch what happens.

 

[haruspex]

Why don't you try it out?
http://www.buero-netshop.de/shop/images/products/main/q-connect-lineal-20cm-kunststoff-transparent.jpg
Hang it ( in the hole, using sewing thread ) and hold it ( at 20cm ). Let it go.

Watch what happens.

This is not a valid test. Yes, over time there will be a motion at A, and the motion will initially be horizontal. But this does not prove that instantaneously there is a horizontal acceleration at A. It could be that the first and second derivatives of x are zero, but the third is positive.

 

[Hesch]

It could be that the first and second derivatives of x are zero, but the third is positive.

If x is the position, I thought that the acceleration ( which is the question ) is the second derivative: d²x/dt².

 

[haruspex]

If x is the position, I thought that the acceleration ( which is the question ) is the second derivative: d²x/dt².

Quite so, but my point is that at t=0 it may be that both $\dot x$ and $\ddot x$ are zero. The first nonzero derivative will surely be positive, but it might be third derivative.

 

[Hesch]

my point is that at t=0 it may be that both x˙\dot x and x¨\ddot x are zero

At t = 0 the acceleration of A will be positive to the right because the thread at A is vertical, thus not yielding any horizontal force ( B is burned ). The rod will begin to rotate clockwise, and the center of the rod will be kept in the same horizontal position. Thus A must accelerate to the right, and B must accelerate to the left.

We are speaking of the acceleration at t = 0+ ?

 

[Vibhor]

At t = 0 the acceleration of A will be positive to the right because the thread at A is vertical, thus not yielding any horizontal force ( B is burned ). The rod will begin to rotate clockwise, and the center of the rod will be kept in the same horizontal position. Thus A must accelerate to the right, and B must accelerate to the left.

This is a possibility . But why must A accelerate to the right only . It can accelerate upwards and B can accelerate downwards such the COM of the rod accelerates downwards ?

Can this be proven mathematically ?

 

[berkeman]

This is a possibility . But why must A accelerate to the right only . It can accelerate upwards and B can accelerate downwards such the COM of the rod accelerates downwards ?

Can this be proven mathematically ?

Can you show us your FBD for t=0+? The sum of torques and forces are non-zero for t=0+. That should help you start to answer this question...

 

[Vibhor]

Can you show us your FBD for t=0+?

Tension acts vertically upwards and weight acts vertically downwards on the rod .

The sum of torques and forces are non-zero for t=0+.

Agreed . But how does that show that particle at A accelerates horizontally ?

 

[berkeman]

Tension acts vertically upwards and weight acts vertically downwards on the rod .
Agreed . But how does that show that particle at A accelerates horizontally ?

You didn't do what I asked. Please post a FBD -- that will answer your questions...

 

[Vibhor]

You didn't do what I asked. Please post a FBD -- that will answer your questions...

Please see the attached picture .

 

[berkeman]

Please see the attached picture .

So given that FBD, what is the sum of forces and sum of moments on the bar?

 

[Vibhor]

So given that FBD, what is the sum of forces and sum of moments on the bar?

Please understand that merely having a net force acting and a net torque around the COM doesn't prove that the particle at A accelerates horizontally .

 

[haruspex]

At t = 0 the acceleration of A will be positive to the right because the thread at A is vertical, thus not yielding any horizontal force ( B is burned ). The rod will begin to rotate clockwise, and the center of the rod will be kept in the same horizontal position. Thus A must accelerate to the right, and B must accelerate to the left.

We are speaking of the acceleration at t = 0+ ?

Consider a particle moving in one dimension according to x=ct³. What is its acceleration at t=0?
However, rereading the question, I see that it seems to be asking about the acceleration at some time marginally greater than zero. This strikes me as strange since offering the two options as either horizontal or none would make more sense at t=0. Moreover, as soon as you allow t>0 there will be a vertically upward acceleration too, making neither answer correct.

Anyway, it is possible to prove there is a nonzero horizontal acceleration even at t=0, but it takes a little more analysis than the observational approach you posted.

 

[Hesch]

rereading the question, I see that it seems to be asking about the acceleration at some time marginally greater than zero.

The problem statement says:

So, what is meant by: "just after this"?

Well, the acceleration = d²x/dt². Now, some physicists think that the time itself is quantified into amounts of ≈ 1E-49s. So if we write:

v(t) = dx(t)/dt

we must add: "assuming dt >> 1E-49s". Otherwise the equation doesn't make sense. So I think that the author by "just after this" means something like "within the next μs".
Should I consider what will happen within the next 1E-52s, I would get crazy. I don't want to get into that discussion due to quantified time.

Moreover, as soon as you allow t>0 there will be a vertically upward acceleration too

I don't understand your conclusion here? As for the vertical accelerations B_acc ≈ g , center_acc ≈ ½g , A_acc = 0.

 

[Chestermiller]

Please understand that merely having a net force acting and a net torque around the COM doesn't prove that the particle at A accelerates horizontally .

If there is a net torque around the COM, what does that tell you about the angular acceleration around the center of mass? How is the velocity of particle A related kinematically to the velocity of the center of mass and the angular velocity (vectorially)?

 

[Vibhor]

Hello Sir ,

Thanks for replying

If there is a net torque around the COM, what does that tell you about the angular acceleration around the center of mass?

There is a net angular acceleration around the center of mass = Net torque / MI

How is the velocity of particle A related kinematically to the velocity of the center of mass and the angular velocity (vectorially)?

$\vec{v}_A = \vec{\omega} \times \vec{r} + \vec{v}_{CM}$

 

[Chestermiller]

$\vec{v}_A = \vec{\omega} \times \vec{r} + \vec{v}_{CM}$

Actually, this is close, but is not quite correct. The correct relationship is:

$$\vec{v}_A = \omega r\vec{i}_θ + \vec{v}_{CM}$$
where $\vec{i}_θ$ is a unit vector in the circumferential (tangential direction). The time derivative of this is the acceleration of particle A. If θ is the angle that the unit vector in the tangential direction makes with the positive x axis, how is the unit vector in the tangential direction related to the unit vectors in the x and y directions?

Chet

 

[Vibhor]

If θ is the angle that the unit vector in the tangential direction makes with the positive x axis, how is the unit vector in the tangential direction related to the unit vectors in the x and y directions?

$\vec{i}_θ = cosθ\hat{i}+sinθ\hat{j}$

 

[Chestermiller]

OK. Now substitute that into the equation for the velocity of particle A and take the time derivative. (You can just leave the time derivative of the center of mass in dv/dt form). What do you get?

Chet

 

[Vibhor]

$\vec{v}_A = \omega rcosθ\hat{i} + \omega r sinθ\hat{j} + \vec{v}_{CM}$

$\vec{a}_A = r[\ddot{\theta}cos\theta - {\dot{\theta}}^2sin\theta]\hat{i} + r[\ddot{\theta}sin\theta + {\dot{\theta}}^2cos\theta]\hat{j} + \dfrac{d\vec{v}_{CM}}{dt}$

 

[Chestermiller]

$\vec{v}_A = \omega rcosθ\hat{i} + \omega r sinθ\hat{j} + \vec{v}_{CM}$

$\vec{a}_A = r[\ddot{\theta}cos\theta - {\dot{\theta}}^2sin\theta]\hat{i} + r[\ddot{\theta}sin\theta + {\dot{\theta}}^2cos\theta]\hat{j} + \dfrac{d\vec{v}_{CM}}{dt}$

What is the value of the angular velocity of the rod at time zero? Substitute this value into your equation for a, and call the angular acceleration α. So what is the acceleration of particle A at time zero in terms of these parameters? What is the horizontal component?

Chet

 

[haruspex]

I don't understand your conclusion here? As for the vertical accelerations B_acc ≈ g , center_acc ≈ ½g , A_acc = 0.

To a first approximation, the acceleration vector at A at a small time t after release is (a, bt²) for nonzero constants a, b.
Specifically, if the radius of inertia of the rod is k, the horizontal distance between A and the mass centre is w, the angle of the rod to the horizontal is theta, and the length of the string at A is r, then $a=\frac{w^2}{w^2+k^2}g\tan(\theta)$, $b=\frac{a^2t^2}r$. (The vertical acceleration is, of course, centripetal.)
It follows that at t=0 there is only a nonzero horizontal acceleration, but that at any later time there is both horizontal and vertical acceleration.

 

[Vibhor]

So what is the acceleration of particle A at time zero in terms of these parameters?

$\vec{a}_A = rcos\theta\alpha\hat{i} + rsin\theta\alpha\hat{j} + \dfrac{d\vec{v}_{CM}}{dt}$

What is the horizontal component?

$\vec{a}_{A,x} = rcos\theta\alpha$

 

[Chestermiller]

$\vec{a}_A = rcos\theta\alpha\hat{i} + rsin\theta\alpha\hat{j} + \dfrac{d\vec{v}_{CM}}{dt}$
$\vec{a}_{A,x} = rcos\theta\alpha$

Good. Nice job.

 

[Vibhor]

But how does that tell us that net acceleration of the particle is in horizontal direction at t=0 ?

We have to find the direction of net acceleration , not its magnitude .

 

[Chestermiller]

But how does that tell us that net acceleration of the particle is in horizontal direction at t=0 ?

We have to find the direction of net acceleration , not its magnitude .

Opps. I lost track of the problem statement. We need to address the vertical component of A's acceleration.
What is the vertical acceleration component of A at time zero?
What is the tension in the left wire at time zero?
What is the vertical acceleration of the center of mass at time zero?
If this is substituted into the equation for the vertical acceleration, what do you get?
(We're not done yet)

Chet

 

[Chestermiller]

PLEASE DISREGARD THIS POST. IT IS BOGUS. THE OP HAD THE ANALYSIS CORRECT IN THE FIRST PLACE. SORRY FOR ANY CONFUSION I MAY HAVE CAUSED. SENIOR MOMENT.

BOTH THE OP's EQUATIONS IN POST # 24 ARE CORRECT, PROVIDED α IS THE ANGULAR ACCELERATION IN THE CLOCKWISE DIRECTION.

Actually, your equation for $\vec{i}_θ$ in post #19 is correct for θ being equal to the angle the rod makes with the negative x-axis (with $\vec{i}_θ$ pointing clockwise), rather than the angle that $\vec{i}_θ$ makes with the positive x axis. Your subsequent equations are correct for this framework. So, we can continue from where we left off.

Chet

 

[Vibhor]

PLEASE DISREGARD THIS POST. IT IS BOGUS.

Which post are you referring to , post#27 or post#28 ?

What should be the next step after post#24 ?

 

[Chestermiller]

Which post are you referring to , post#27 or post#28 ?

Post #28.

What should be the next step after post#24 ?

See post #27. By the way, this is likely to get a little tricky. I don't think the person who conceived of this problem realized how complicated it is.

Chet