- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How do I solve a Series RLC circuit?
- Thread starter wiz0r
- Start date
-
- Tags
- Circuit Rlc Rlc circuit Series
In summary: I'll come back and give a more detailed and comprehensive review after I've had a chance to play with the software more.
Physics news on Phys.org
- #2
technician
- 1,506
- 18
I think you need to know the frequency of the supply to get started... do you have it?
- #3
wiz0r
- 57
- 0
technician said:I think you need to know the frequency of the supply to get started... do you have it?
The source is just a DC source... so, there's no frequency.
- #4
technician
- 1,506
- 18
my apologies... I thought it was an AC circuit
- #5
gneill
Mentor
- 20,989
- 2,933
Hi wiz0r,
Presumably the initial conditions that you're looking for is the state of the circuit at the time t=0+ when the switch has just opened.
Immediately before the switch opens, and assuming that the switch had been closed for "a long time", then your statement that the capacitor will look like an open circuit is correct -- no current will flow into or out of it. Similarly, the inductor will look like a short circuit.
Can you determine what voltage should be across the capacitor at t=0-?
Presumably the initial conditions that you're looking for is the state of the circuit at the time t=0+ when the switch has just opened.
Immediately before the switch opens, and assuming that the switch had been closed for "a long time", then your statement that the capacitor will look like an open circuit is correct -- no current will flow into or out of it. Similarly, the inductor will look like a short circuit.
Can you determine what voltage should be across the capacitor at t=0-?
- #6
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #7
gneill
Mentor
- 20,989
- 2,933
wiz0r said:Assuming the switch is closed and the capacitor creates an open circuit... I'd have the source with the 10 and 60 ohm resistors... Using voltage divider I find that
Vc(0-) = Vc(0+) = 25.71 V, right?
That looks fine. So when the switch opens the capacitor will have that voltage on it as an initial condition. And the current will still be zero because of the inductor.
To find i(t) you'll have to either write and solve the differential equation for the new circuit configuration, or use a "canned" solution for the RLC circuit.
- #8
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #9
gneill
Mentor
- 20,989
- 2,933
wiz0r said:Alright.. sounds good.. I'll write what I have.. can you comment/guide me through it and point out any errors? Please...
Now as t = infinity...
i(inf) = 0... right? since the capacitor will act as an open circuit...
Now as for using KVL... after the initial differentiation of the KVL I get...
L d2i(t)/dt2 + R di(t)/dt + i(t)/C = 0
2.5 d2i(t)/dt2 + 120 di(t)/dt + i(t)/1m = 0
Now.. if I divide the equation by 2.5 I get..
d2i(t)/d2t + 48 di(t)/dt + 400 i(t) = 0
damping ratio = (48/2)/sqrt(400) = 1.2
since damping ratio > 1... circuit is overdamped...
s1 = -10.73
s2 = -37.26
i(t) = K1 e^(-10.73 t) + K2 e^(-37.26 t)
Ok... how about now? Any errors...??
It's looking good!
- #10
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #11
gneill
Mentor
- 20,989
- 2,933
The equation should yield current values, and Vc(0) is a voltage.
At time t = 0 the current is zero, so K1 + K2 = 0. That is, K1 = -K2. You'll need to find another way to solve for the values. Perhaps if you could determine the initial rate of change of the current...
At time t = 0 the current is zero, so K1 + K2 = 0. That is, K1 = -K2. You'll need to find another way to solve for the values. Perhaps if you could determine the initial rate of change of the current...
Last edited:
- #12
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #13
gneill
Mentor
- 20,989
- 2,933
Rightwiz0r said:Okay.. btw, you meant that K1 = - K2.. right?

so the initial rate of change of the current...
take the derivative of
i(t) = K1 e^(s1 * t) + K2 e^(s2 * t)
at t = 0.. gives
s1K1 + s2K2 = 0... which is what I had before and it was wrong... any other hint..?
s1K1 + s2K2 won't be zero. It'll equal the initial rate of change of the current. Go back to the circuit diagram and see if you can't determine what that might be. You've an inductor that has suddenly had a voltage Vc impressed upon it... how will it react?
- #14
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #15
gneill
Mentor
- 20,989
- 2,933
wiz0r said:The voltage of the inductor at t=0+ should be equal to:
VL(0+) = - Vc(0+) = -25.71, right?
Which implies that
di(0+)/dt = -25.71, Thus we can write that:
s1K1 + s2K2 = -25.71
K1 = -K2
K1 = -0.97 and K2 = 0.97, yes/no/maybe?
Sorry, I'm really tired.. >.<
The equation of interest for the inductor is its defining equation: V = L dI/dt. In this case there's an impressed voltage Vc across inductor L=2.5H. What's dI/dt?
- #16
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #17
gneill
Mentor
- 20,989
- 2,933
wiz0r said:dI/dt = Vc/L ?
dI/dt = 25.71/2.5 ?
dI/dt = 10.28?
Right. At t=0 dI/dt = Vc/L = 10.286 A/s. So, given K1 = -K2,...
- #18
wiz0r
- 57
- 0
Edited for assignment purposes...
Last edited:
- #19
gneill
Mentor
- 20,989
- 2,933
wiz0r said:and s1K1 + s2K2 = 10.286...
K1 = 0.388 and K2 = -0.388
Therefore...
i(t) = 0.388e^(-10.73 * t) + -0.388e^(-37.26 * t)
? =0
Looks good! Bravo!
- #20
wiz0r
- 57
- 0
gneill said:Looks good! Bravo!
Woohoo... thank you so much!
One last thing... I'm told to make a plot of i(t).. to do that I used SPICE(attachment)... does the graph looks OK (attachment)?
@all other people: If anyone reading is taking the class with Rosado please say hi!
Attachments
- #21
gneill
Mentor
- 20,989
- 2,933
Looks okay. I think if you made the maximum timestep a bit smaller you might resolve the peak a bit better (eliminate the "flat bottom").
Here's the plot of the mathematical version:
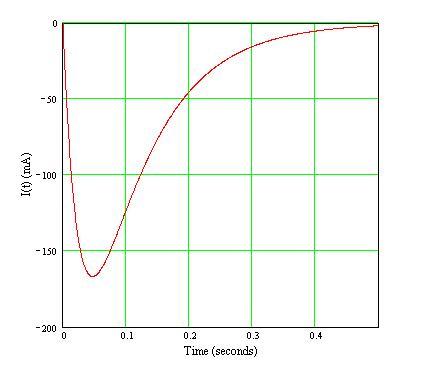
I've negated the current values ( -I(t) ) in order to match your Spice model current direction.
Here's the plot of the mathematical version:
I've negated the current values ( -I(t) ) in order to match your Spice model current direction.
Attachments
- #22
wiz0r
- 57
- 0
gneill said:Looks okay. I think if you made the maximum timestep a bit smaller you might resolve the peak a bit better (eliminate the "flat bottom".
Here's the plot of the mathematical version:
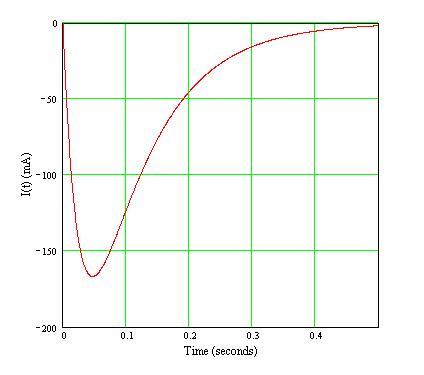
I've negated the current values ( -I(t) ) in order to match your Spice model current direction.
Perfect... thank you so much... I owe you big time... If I can repay you with something (except money.. I'm poor!) let me know! :)
- #23
gneill
Mentor
- 20,989
- 2,933
wiz0r said:Perfect... thank you so much... I owe you big time... If I can repay you with something (except money.. I'm poor!) let me know! :)
You're quite welcome. Just go get an "A" in your course!
- #24
wiz0r
- 57
- 0
gneill said:You're quite welcome. Just go get an "A" in your course!
I will definitely try my best. :)
Thank you so much. Bye bye for now. :)
Edwin
FAQ: How do I solve a Series RLC circuit?
What is a Series RLC circuit?
A Series RLC circuit is an electrical circuit that contains a resistor (R), an inductor (L), and a capacitor (C) connected in series. It is also known as a second-order circuit and is commonly used in electronic filters and oscillators.
What is the purpose of a Series RLC circuit?
The purpose of a Series RLC circuit is to control the flow of current in an electric circuit. The resistor, inductor, and capacitor work together to create a filter that can either block or pass certain frequencies, making it useful for various applications such as signal processing and frequency selection.
How does a Series RLC circuit behave in different frequencies?
In a Series RLC circuit, the behavior can vary depending on the frequency of the input signal. At low frequencies, the inductor has a higher impedance, and the circuit behaves like a high-pass filter. At high frequencies, the capacitor has a lower impedance, and the circuit behaves like a low-pass filter. At a certain resonant frequency, the impedance of the inductor and capacitor cancel out, resulting in a high impedance and a sharp response.
How do I calculate the resonant frequency of a Series RLC circuit?
The resonant frequency of a Series RLC circuit can be calculated using the formula: fr = 1/(2π√(LC)), where fr is the resonant frequency, L is the inductance in henries, and C is the capacitance in farads.
What is the difference between a Series RLC circuit and a parallel RLC circuit?
A Series RLC circuit has the components connected in series, whereas a parallel RLC circuit has the components connected in parallel. This means that the voltage across each component in a Series RLC circuit is the same, while the current through each component in a parallel RLC circuit is the same. Additionally, the resonant frequency of a parallel RLC circuit is calculated using the formula: fr = 1/(2π√(LC)), where fr is the resonant frequency, L is the inductance in henries, and C is the capacitance in farads.
Similar threads
- Replies
- 3
- Views
- 2K
- Replies
- 15
- Views
- 5K
- Replies
- 6
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 12
- Views
- 5K
- Replies
- 3
- Views
- 2K
- Replies
- 8
- Views
- 861
- Replies
- 6
- Views
- 2K
- Replies
- 3
- Views
- 3K
Share:


