- #1
laymanhobbist
- 29
- 2
i need a bit of help ...
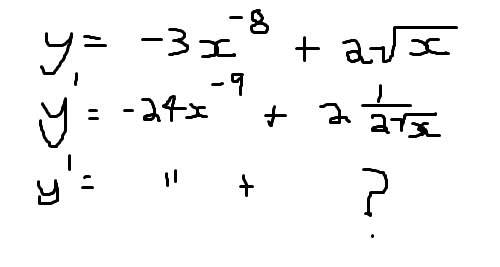
so here ...
y = f(x) means .. that ?
Suppose you want to calculate the derivative of a curve at some particular point. Draw a tangent to the curve at that point. The slope of the tangent gives you the derivative. This is geometrical approach.
The algebraical approach is little different. Let y =f(x) which means y is a function of x. A very small change in y is denoted by dy and a very small change in x is denoted by dx. The derivative of y means the amount by which y changes if x changes in a very short extent. So mathematically it is given by dy/dx.
so here ...
y = f(x) means .. that ?