How Do You Design a Resistive Ladder with Specific Voltage Outputs and Ratios?

[Eric08]

Homework Statement

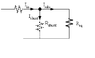
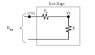
Design a resistive ladder so that, when driven by a 1000V source, yields the voltages 100v, 10v, 1v, 100mv, 10mv, and 1 mv under the following constraints

(A) the equivalent resistance seen by the source must be 1 Mega-ohm.

(B) the current entering each node must split between the subsequent series and shunt the resistances in a 3 to 1 ratio.

Homework Equations

The Attempt at a Solution

I attempted to start the design of this ladder but I am not sure how to choose my resistances so that the equivalent is the 1 Mega-ohm. Also, what do they mean in part B of this question by shunting the resistances into a 3 to 1 ratio?

 

[Eric08]

This is my attempt so far at the design. Am I on the right track? I am kind of confused here.

-Thank You

 

[gneill]

Have you covered any "canned" methodology for designing resistor ladders in your coursework? If not, there's going to be a bit of number crunching to do.

I'd start at the tail of the ladder and work back towards the voltage source. The last section is a simple voltage divider, so assign R to that last resistor and 9R to the second to last one (the final horizontal resistor). That'll give you a 10:1 division of the voltage presented by the previous stage. For purposes of design, just assign 1 Ohm to R for now.

Next you'll have to work out an algorithm for building the previous stage. You have a voltage division constraint (divide by ten) and a current division constraint (3 to 1), along with the resistance of the already chosen tail stage. Keep track of the total resistance as you work back, stage by stage.

When you're done you'll have filled in place-holder values for all the resistors, and will have the total resistance as seen by the source (since you kept track of it as you worked back). The total resistance won't be 1M Ohm. Can you determine how to scale the resistance values to make it 1M?

 

[VitaX]

I have a problem very similar to this on my homework as well.

What I did for part a) was this:

Req = R/k and k must be 0.1 in this problem for part a while Req must be 1000 Ohms. So I solved for R and got R = 100 Ohms. Then I used these equations to find R1 and R2:

R1 = R(1-k)/k = 900 Ohms
R2 = R/(1-k) = 111.11 Ohms

I got these equations from my book.

But I'm a bit confused on part b, because nothing is really stated about current in resistance ladders in the book. What does it want us to do exactly on part b? Sorry for hijacking your thread but I used your numbers in the calculations for part a) if that helps out (Hopefully it is right).

My drawing of it:
[PLAIN]http://img687.imageshack.us/img687/5123/reistanceladder.png

 

[gneill]

But I'm a bit confused on part b, because nothing is really stated about current in resistance ladders in the book. What does it want us to do exactly on part b? Sorry for hijacking your thread but I used your numbers in the calculations for part a) if that helps out (Hopefully it is right).

Presumably the criterion in (B) means that each shunt resistor will be three times the equivalent resistance of the rest of the network. In this diagram R_shunt is part of a new stage being added. R_eq is the current equivalent resistance of the stages to the right of this new construction.

So that I_subs = 3 x I_shunt. This forces the choice of R_shunt.

 

[VitaX]

Presumably the criterion in (B) means that each shunt resistor will be three times the equivalent resistance of the rest of the network. In this diagram R_shunt is part of a new stage being added. R_eq is the current equivalent resistance of the stages to the right of this new construction.

So that I_subs = 3 x I_shunt. This forces the choice of R_shunt.

So for part b) you disregard all your work for pat a) as they are completely separate? I understand what you are saying when you're talking about the resistors and current and how they are related but is the problem asking to find R1, R2, R, I, K, and Req all over again?

 

[gneill]

So for part b) you disregard all your work for pat a) as they are completely separate? I understand what you are saying when you're talking about the resistors and current and how they are related but is the problem asking to find R1, R2, R, I, K, and Req all over again?

It could well be that the problem as given is not amenable to using a 'canned' solution from another problem. The current division criteria might be a show stopper for that.

This would force the student to develop his own method for designing the stages, one that incorporated the design requirements: (A), (B), and the 10x per-stage voltage division.

 

[VitaX]

It could well be that the problem as given is not amenable to using a 'canned' solution from another problem. The current division criteria might be a show stopper for that.

This would force the student to develop his own method for designing the stages, one that incorporated the design requirements: (A), (B), and the 10x per-stage voltage division.

My teacher just emailed me back saying I need to develop separate circuit designs for part a) and b). So I guess I use the same design I drew up, but I have to find different Reistor values. But how exactly would I do that? Sorry if I seem like I'm repeating myself, I just can't find any good examples of resistive ladders online.

 

[gneill]

My teacher just emailed me back saying I need to develop separate circuit designs for part a) and b). So I guess I use the same design I drew up, but I have to find different Reistor values. But how exactly would I do that? Sorry if I seem like I'm repeating myself, I just can't find any good examples of resistive ladders online.

You can build a single ladder incorporating all of the criteria. Start by designing the final stage, which is simply a voltage divider that takes the next to last stage's voltage and divides by ten. Big hint: For now, assign a value of R = 1 Ohm to the final resistor. That'll be the value that all other resistors will scale to.

Next see what has to be done to add the next stage. For example, the shunt resistor has a requirement based upon the current division spec. How can you enforce it by choice of the stage shunt resistor? The new stage is a voltage divider, too. So how can you choose the resistor value for R_a?