- #1
bill.connelly
- 21
- 0
Hi,
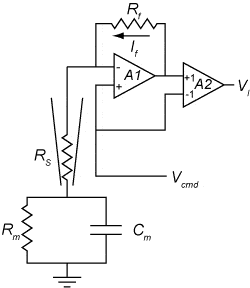
I'm just a humble biologist (writting up a PhD Thesis in Neuroscience) and I'm trying to get a feel for how my equipment works. The circuit for monitoring the current that flows across a cells membrane (in response to an imposed voltage step) can essentially be seen as a resistor, connected to a resistor and capacitor in parallel (Rs, Rm and Cm)
(the full circuit, ignore the op-amps and such if you can)
I understand that for a resistor and capacitor in parallel, the current that flows in response to a voltage can be explained by
[tex]
i(t)=\frac{v(t)}{R}+C\frac{dv(t)}{dt}
[/tex]
However this means that in response to a step change in voltage, I = infinity (which is of course what you expect). With a resistor in series to that parallel circuit, I also appreciate that at after a step of voltage V,
[tex]\Delta I=V.R_{s}[/tex]
and then I recays exponentially to
[tex]\Delta I=V.(R_{s}+R_{m})[/tex]
However, I want to be able to calculate I and any time, in response to an arbitrary voltage. Can anyone explain, or even just give me the equation to calculate that.
I'm just a humble biologist (writting up a PhD Thesis in Neuroscience) and I'm trying to get a feel for how my equipment works. The circuit for monitoring the current that flows across a cells membrane (in response to an imposed voltage step) can essentially be seen as a resistor, connected to a resistor and capacitor in parallel (Rs, Rm and Cm)
(the full circuit, ignore the op-amps and such if you can)
I understand that for a resistor and capacitor in parallel, the current that flows in response to a voltage can be explained by
[tex]
i(t)=\frac{v(t)}{R}+C\frac{dv(t)}{dt}
[/tex]
However this means that in response to a step change in voltage, I = infinity (which is of course what you expect). With a resistor in series to that parallel circuit, I also appreciate that at after a step of voltage V,
[tex]\Delta I=V.R_{s}[/tex]
and then I recays exponentially to
[tex]\Delta I=V.(R_{s}+R_{m})[/tex]
However, I want to be able to calculate I and any time, in response to an arbitrary voltage. Can anyone explain, or even just give me the equation to calculate that.