- #1
ASUengineer16
- 5
- 0
Homework Statement
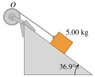
A block with mass m = 5.00 kg slides down a surface inclined 36.9 degrees to the horizontal (the figure View Figure ). The coefficient of kinetic friction is 0.23. A string attached to the block is wrapped around a flywheel on a fixed axis at O. The flywheel has mass 28.0 kg and moment of inertia 0.500 kg*m^2 with respect to the axis of rotation. The string pulls without slipping at a perpendicular distance of 0.200 m from that axis.
Homework Equations
I tied solving for the sum of torques, which is T*r=I*([tex]\alpha[/tex]) where T is the tension and r is the radius of the pulley, .200 m. I think solved for T for the box. Once solving for T I got, T=mg(sin(theta)-cos(theta)*[tex]\mu[/tex]k)-m*a. Then using the rule, [tex]\alpha[/tex]=a/r, I then substituted a/r for all the [tex]\alpha[/tex]'s and then plugged my T for the torque equation into the T from the force equation.
In the end I came up with the equation:
mg(sin(theta)-cos(theta)*[tex]\mu[/tex]k)-m*a = (I*a)/r^2
This yeilded me the wrong answer and I have no idea where I am wrong. I have a feeling it has to do with the mass of the pulley since it was given, but I am not sure how to relate it to the problem since they give you the moment of inertia for the pulley ?
Any help would be great thanks !