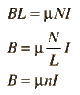How Does the Radius Affect the Magnetic Field Inside a Solenoid?

[Chip90]

Homework Statement

There is an infinetly long solenoid with current I, radius R, and N loops/unit length. Find the B field in the axis of the solenoid.

Homework Equations

The Attempt at a Solution

So that eq. can be narrowed to

B integral dl = Uo I

the only problem is I can't find dl its not 2*pi*R, 2r, 2RN... I am not sure what's wrong here.

I've made a similar diagram where the two edges and the side on the outside have a B field of 0.

Any ideas?

 

[Chip90]

any ideas? I also got
'

but now sure how they got that from amperes law? ir is that the answer? thanks.

 

[Schecter5150]

That's correct. The differential length is simply L when integrated, since the magnetic field runs parallel to the axis of the solenoid. The enclosed current Ienc is the current I running through each turn multiplied by the number of turns in the solenoid, or N*I.

Hopefully that helps.

 

[Chip90]

so in Amperes law.. dl= N*I ? How do I factor in the radius then? Or does it not matter?

nvm i see that your saying that Ienc= I*N correct?

but I am still left with R? How do I factor that in?

 

[Schecter5150]

so in Amperes law.. dl= N*I ? How do I factor in the radius then? Or does it not matter?

nvm i see that your saying that Ienc= I*N correct?

but I am still left with R? How do I factor that in?

You draw the gaussian loop enclosing only half of the inside of the solenoid and the other half s outside. There is no "r" because dl = L when integrated over the length of the solenoid.

Because B does not depend on the radius of the solenoid, the B field inside the solenoid is uniform, much like the E-field between a parallel plate capacitor is uniform.

 

[Chip90]

ahha that makes sense.. thanks!

 

[cdotter]

so in Amperes law.. dl= N*I ? How do I factor in the radius then? Or does it not matter?

nvm i see that your saying that Ienc= I*N correct?

but I am still left with R? How do I factor that in?

The vertical components don't matter since it's a dot product. The length outside of the solenoid is infinitely far away. At a point infinitely far away the magnetic field is 0, therefore it doesn't matter. That leaves the only important part as the horizontal line inside the solenoid. Therefore it's simply L (or X in this case.)