How Is Angular Momentum Calculated in a Pulley System?

[fogvajarash]

Homework Statement

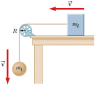
In the graph shown in the picture, an expression for the acceleration of the pulleys is obtained.

Homework Equations

The Attempt at a Solution

The thing i don't understand is, how do we find the angular momentum for the system? In class, I was told that the angular momentum for the system was:

L_tot = MvR + m¹vR + m<sup>2vR

However, why do we pick the same velocities for the objects? (aren't they accelerating, and thus having different velocities?). As well, why do we choose the radius of the pulley for mass 1 and mass 2 to be that way? (isn't angular momentum calculated for objects in linear motion as the distance from the origin, which in this case is the axle of the pulley?).

Thank you very much.</sup>

 

[Mentz114]

Non-spinning objects traveling in straight lines have no angular momentum (AM). AM is the rotational equivalent of momentum, p = m v, so AM = I ω where I is the moment of inertia and ω is the angular speed ( radians / sec ). I think the only AM in the setup here is in the pulley wheel.

The weights have the same speed because the cord is inelastic.

 

[fogvajarash]

Non-spinning objects traveling in straight lines have no angular momentum (AM). AM is the rotational equivalent of momentum, p = m v, so AM = I ω where I is the moment of inertia and ω is the angular speed ( radians / sec ). I think the only AM in the setup here is in the pulley wheel.

The weights have the same speed because the cord is inelastic.

What does it mean by inelastic? So i suppose it's given in the problem? (What i thought was that the accelerations were the same). Moreover, I'm not sure on the angular momentum part. Can someone shed some light on this?

 

[haruspex]

Non-spinning objects traveling in straight lines have no angular momentum (AM).

This is not correct. Angular momentum depends on the reference point. An object moving in a straight line also has angular momentum about any reference point not in its line of travel. It's the product of the linear momentum and the orthogonal displacement. In this case, that distance is the radius of the wheel.

 

[Mentz114]

This is not correct. Angular momentum depends on the reference point. An object moving in a straight line also has angular momentum about any reference point not in its line of travel. It's the product of the linear momentum and the orthogonal displacement. In this case, that distance is the radius of the wheel.

I'm sorry I misled the OP. I'm sufficiently embarassed to withdraw from homework helping for a while, so huruspex won't have to check and correct my attempts.

 

[fogvajarash]

I have been revising this amd came to the conclusion that it's the radius as we are looking for rFsin0 (0 is the angle between r and F) so this is simply R. However, why are the velocities the same? In pulleys, wasn't acceleration the only constrained variable? (Or are we looking at an instant of time?)

 

[haruspex]

I have been revising this amd came to the conclusion that it's the radius as we are looking for rFsin0 (0 is the angle between r and F) so this is simply R. However, why are the velocities the same? In pulleys, wasn't acceleration the only constrained variable? (Or are we looking at an instant of time?)

If two objects start from rest at the same time and have the same accelerations at all times then they will have the same velocities at all times (and will have the same displacements at all times).