- #36
mathmari
Gold Member
MHB
- 5,049
- 7
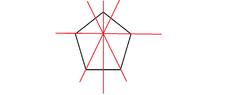
I like Serena said:Take a look at $D_6$:The axis of symmetry of $s$ in this picture goes through $2$ beads.
The axis of $rs$ goes through $0$ beads. (Thinking)
I got stuck right now... Isn't $m$ constant in this example, $m=6$ ? (Wondering)
How can we take cases if $m$ is odd or even? (Wondering)