- #1
Physicsfreek
- 4
- 0
I need the formula for the length of vectors x, y and z as vector f rotates in plane R.
What is the length of each vector (x, y and z) when vector f is at x degrees? Vector f extends from zero, rotates in plane R and has a unit length of 1.

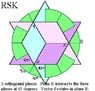
Rotational energy is an influence on, and/or is a product of, the random chance that an event will happen. In the quantum world, particles can diffuse into waveforms and the waveform is a cyclic probability pattern. A wave pattern can be expressed as the sum of axial vectors around an equilibrium position and, in the dimensional space of RSK, the order of vector addition matters.
RSK is intersected through zero by the forth-dimensional axis, Tk. Frequency vector f rotates around and is perpendicular to Tk.
Frequency vector f has a magnitude of one unit and is set as a unit vector. Vector f is the sum of three vectors in three different orientations:
(vector x + vector y + vector z)1 = vector f
(vector y + vector z + vector x)2 = vector f
(vector z + vector x + vector y)3 = vector f
The addition of the three vectors in the three different orientations may arrive at the same place within RSK, but the dimensional structure of the vector addition to a point is different for each orientation.
The orientations of the planes are designated as 1, 2 and 3. Within each plane of each orientation, after one revolution of vector f., the sum of the two vectors, (vector x + vector y)1, (vector y + vector z)2 and (vector z + vector x)3, transcribe an ellipse within the respective plane.

RSK is comprised of three different, three dimensional orientations: (vector x + vector y + vector z)1, (vector y + vector z + vector x)2 and (vector z + vector x + vector y)3.
The sum of the three vectors in each orientation follows the rotation of vector f in plane R. With a full rotation of vector f, the sum of the first two vectors in each plane transcribes an ellipse within that plane. The third vector extends from the edge of the ellipse and is parallel to the third axis to the tip of vector f.

Reference System K is the basis for "The Theory of the 42s." The Theory of the 42s may be stated as manifestations of energy in deterministic states that form the structure of electrons and quarks. These determinate states can be projected with iterated equations within a 42. Three 42s combine in RSK. See http://www.ReferenceSystemK.com
What is the length of each vector (x, y and z) when vector f is at x degrees? Vector f extends from zero, rotates in plane R and has a unit length of 1.
Rotational energy is an influence on, and/or is a product of, the random chance that an event will happen. In the quantum world, particles can diffuse into waveforms and the waveform is a cyclic probability pattern. A wave pattern can be expressed as the sum of axial vectors around an equilibrium position and, in the dimensional space of RSK, the order of vector addition matters.
RSK is intersected through zero by the forth-dimensional axis, Tk. Frequency vector f rotates around and is perpendicular to Tk.
Frequency vector f has a magnitude of one unit and is set as a unit vector. Vector f is the sum of three vectors in three different orientations:
(vector x + vector y + vector z)1 = vector f
(vector y + vector z + vector x)2 = vector f
(vector z + vector x + vector y)3 = vector f
The addition of the three vectors in the three different orientations may arrive at the same place within RSK, but the dimensional structure of the vector addition to a point is different for each orientation.
The orientations of the planes are designated as 1, 2 and 3. Within each plane of each orientation, after one revolution of vector f., the sum of the two vectors, (vector x + vector y)1, (vector y + vector z)2 and (vector z + vector x)3, transcribe an ellipse within the respective plane.
RSK is comprised of three different, three dimensional orientations: (vector x + vector y + vector z)1, (vector y + vector z + vector x)2 and (vector z + vector x + vector y)3.
The sum of the three vectors in each orientation follows the rotation of vector f in plane R. With a full rotation of vector f, the sum of the first two vectors in each plane transcribes an ellipse within that plane. The third vector extends from the edge of the ellipse and is parallel to the third axis to the tip of vector f.
Reference System K is the basis for "The Theory of the 42s." The Theory of the 42s may be stated as manifestations of energy in deterministic states that form the structure of electrons and quarks. These determinate states can be projected with iterated equations within a 42. Three 42s combine in RSK. See http://www.ReferenceSystemK.com
Attachments
Last edited by a moderator: