Minimal Dimensions for Maximum Bending Moment

[Sumdog]

Hi

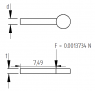
Please can someone help me calculate the minimal thickness and width that will resist bending in each of the aluminium beams that are fixed on one end and support a 0.0013734 Newton load on the other.

The axis passes through the center of the octagonal shape and goes into the page. All measurements are in millimeters.

By referring to the attachment: t and d need to be minimized to a size that will not allow bending.

Thank you for your help

 

[SteamKing]

I'm not certain that static bending is the limiting factor. Your diagram indicates that this object will spin at 15000 RPM. Such a speed will introduce significant dynamic loading on the magnets and their attachments to the hub.

 

[Sumdog]

Thanks for the reply

That's what I thought but when I spoke to my mechanics lecturer, he said that dynamic forces will not effect the bending of the beam because the dynamic forces will act along the beam towards the center axis. Therefore it is a static bending moment problem.

How would you go about solving for t and d?

 

[SteamKing]

When you have an object like the one in your picture rotating at 15000 RPM, the magnets will want to fly off the spokes due to the centrifugal loads set up by the rotation. It's still not clear to me that bending will be the limiting factor

 

[Sumdog]

I realize the magnet will fly off if it is not secured properly. We need to assume that the magnet is secured onto the beam so that it will not come off.

According to my lecturer, the minimum values for t and d that will resist bending must be solved for using:

σ = Mc/I

M = the resultant moment about the fixed point
c = the perpendicular distance from the neutral axis to the surface of the beam i.e t/2
I = the moment of inertia

and I get the following equation:

95Mpa = (1.441 x10^-5)(c) / (1/12)(d)(2c)^3