Normal force on block placed on incline.2 approaches different result

[Curieuse]

Homework Statement

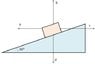
The problem wants me to order the choice for the directions of a force F of a constant magnitude F(a,b,c,d are unit vectors along which F has to be oriented) exerted on the block placed on an incline at 30° to the horizontal based on the normal force F_n that the incline would exert on the block in each case. attached: w.jpg is the pic with the question

2. The attempt at a solution
I've attempted this from two coordinate frames! One inclined with the plane and the other horizontally aligned with the base of the incline! And I get the solutions as attached! I want to know why the question marked approach gives haywire answers! The other approach is for reference!
The first is the legit answer and the next one is easier because of the chosen orientation of the frame of reference but the results are illogical. Why?
0002 is the legit answer and 0003 is the illogical one

 

[PhanthomJay]

attachments did not post

 

[Curieuse]

Please right click on the images and open in a new tab. that must help!

 

[PhanthomJay]

I am not sure what you are trying to find. The normal force acts perpendicular to the incline no matter what reference axes you choose.
The normal force is mgcostheta no matter what reference axes you choose. You can find components of that force in the horiz and vert directions if you want. It is a little messy when you choose horiz and vert axes instead of choosing the x-axis parallel to incline and y-axis perp to incline.when so doing, the normal force has an x comp of Nsintheta left and Ncostheta up.

 

[Curieuse]

Yes. That's exactly the glitch i found. And about the problem statement which i messed up.. I quote:
"Figure w.jpg shows four choices for the direction of a force of magnitude F to be applied to a block on an inclined plane. The directions are either horizontal or vertical.(For choices a and b, the force is not enough to lift the block off the plane). Rank the choices according to the magnitude of the normal force on the block from the plane- greatest first." And I arrived at the order d>c>a>b, which seems logically legit. The illogical one is tormenting.
As far as the 'a' choice in direction is considered, I see that the horizontal components:
F+F_Nsin 30°=0
This i think is messed up because, as the acceleration in the x direction is zero and the two forces acting to the left do not have magnitudes as equal to zero, there must be some force that is the negative vector of the resultant due to these above forces acting on the body to cancel stuff out so that there's no acceleration in the horizontal way.. I wonder what that force would be, because clearly the normal force doesn't have any components in a direction opposite to F leave alone the fact that the component is in the same direction as F.

 

[Doc Al]

No matter which set of axes you choose, the acceleration can only be parallel to the surface. Thus, if you use axes oriented horizontally and vertically, realize that each of those axes will have a component of acceleration. (That's why using axes parallel and perpendicular to the surface is easier. No acceleration perpendicular to the surface.)

 

[Curieuse]

Thanks Doc al! I didn't see that the block could accelerate well. :P

 

[Doc Al]

Thanks Doc al! I didn't see that the block could accelerate well. :P

:thumbs: