- #1
Delzac
- 389
- 0
Hi all,
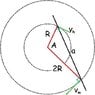
The minute hand of a church clock is twice as long as the hour hand. At what time after mid-night does the end of the minute hand move away from the end of the hour hand at the fastest rate?
I totally dun have a clue on how to do this any hints??
By thw way what is linear speed?
The minute hand of a church clock is twice as long as the hour hand. At what time after mid-night does the end of the minute hand move away from the end of the hour hand at the fastest rate?
I totally dun have a clue on how to do this any hints??
By thw way what is linear speed?
Last edited: