- #1
Dante Tufano
- 34
- 0
In the figure below, two springs are attached to a block that can oscillate over a floor. If the left spring is removed, the block oscillates at a frequency of 27 Hz. If, instead, the spring on the right is removed, the block oscillates at a frequency of 43 Hz. At what frequency does the block oscillate with both springs attached?
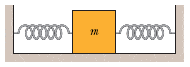
So I know that f=(1/2pi)*sqrt(k/m)
k=((2*pi*f)^2)
Using these formulas, I solved for each coefficient of friction. Then, I used 1/k= 1/k1 +1/k2 to find the total k value. I plugged that into the frequency equation and got 22.866 Hz. However, webassign tells me that's wrong. Any ideas on where I screwed up? I only have one try left.
So I know that f=(1/2pi)*sqrt(k/m)
k=((2*pi*f)^2)
Using these formulas, I solved for each coefficient of friction. Then, I used 1/k= 1/k1 +1/k2 to find the total k value. I plugged that into the frequency equation and got 22.866 Hz. However, webassign tells me that's wrong. Any ideas on where I screwed up? I only have one try left.