- #1
MiniTank
- 62
- 0
how exactly do you go from a graph of a function to plotting the graph of the derivative of its function?
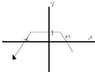
ex: y=f(x) .. this is just the general shape with the intercepts(check the attatchment)
im not sure but when going from the original function to its derivative, does the function lose a turning point, making this a straight line?
ex: y=f(x) .. this is just the general shape with the intercepts(check the attatchment)
im not sure but when going from the original function to its derivative, does the function lose a turning point, making this a straight line?
Attachments
Last edited: