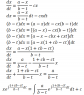- #1
Irid
- 207
- 1
I have a differential equation
[tex]
\frac{dx}{dt} = \frac{a-x}{b-t} - cx
[/tex]
but no idea if there is an analytical solution :(
I tried the integrating factor method, but I run into a e^(-x)/x^2 kind of integral, which I think doesn't have an analytical expression.. Help, please?
[tex]
\frac{dx}{dt} = \frac{a-x}{b-t} - cx
[/tex]
but no idea if there is an analytical solution :(
I tried the integrating factor method, but I run into a e^(-x)/x^2 kind of integral, which I think doesn't have an analytical expression.. Help, please?