- #36
gneill
Mentor
- 20,989
- 2,933
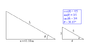
Lolagoeslala said:y = gt^2/2
Okay. Now, is y increasing or decreasing in value as time moves forward? (Is the skier rising or falling?)