- #1
A.Q
- 8
- 0
Software assignment -- Evaluate the limit & compare the series
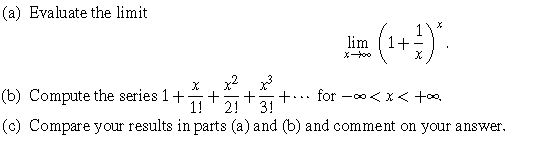
In part a, I used Microsoft mathematics and found it e
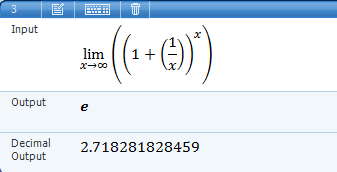
In part b, I used [itex]\sum[/itex] but I can't find the right formula
I don't want an easy answer but I really have no idea about part b, it's not even in the textbook
Homework Statement
Homework Equations
The Attempt at a Solution
In part a, I used Microsoft mathematics and found it e
In part b, I used [itex]\sum[/itex] but I can't find the right formula
I don't want an easy answer but I really have no idea about part b, it's not even in the textbook