Solving a Complex Circuit Problem with Kirchhoff's Laws

[mopar969]

Please see attachment for problem. I know Kirchhoff laws and resistors in parallel and series but how do you solve this?

 

[mopar969]

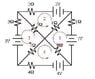
I thought that maybe I could use kirckoffs laws for this problem but I am unsure if this is a good idea to start?

 

[ehild]

Is there a nodal point in the middle of the circuit?

Yes, it is a good idea to apply Kirchhoff's rules.

ehild

 

[mopar969]

Since there is a point in the middle of the circuit where all the voltages meet what will be the currents for the four loops and the outer loop?

 

[gneill]

Since there is a point in the middle of the circuit where all the voltages meet what will be the currents for the four loops and the outer loop?

Isn't that what you're supposed to calculate? There are four loops, so you can write four equations in four unknowns to find the loop currents. Then use the loop currents to determine the individual currents in the components.

 

[mopar969]

I am having trouble knowing what junctions to substitute into what loop equations.
Here are my equations:
Junctions:
J1:I2=I6+I1
J2:I3=I2+I5
J3:I1+I8=I4
J4:I4+I7=I3
J5:I5+I6=I7+I8

Loops:
L1:1=-I1+6I6+8I8
L2:2=-2I2+5I5-6I6
L3:3=-3I3-7I7-5I5
L4:4=-4I4-8I8+7I7
L5:10=-4I4-I1-2I2-3I3

Can you give a hint on where to start for a substitution in this problem?

 

[gneill]

I am having trouble knowing what junctions to substitute into what loop equations.

<snip>

Can you give a hint on where to start for a substitution in this problem?

I suggest that you write KVL equations for the loops. That is, you know that the sum of the voltage rises and drops around any given loop is zero. Attached you'll find my suggestion for the choice of loops.

 

[mopar969]

My first four loops are the same as your pic. My fifth loop is just around the outside perimeter. I was just curious if you could give me a hint on where to start my substitution to get something to cancel?

 

[gneill]

I understand, but it would be simpler to write just the four equations pertaining to the loops that I indicated with the red arrows. Each of those red arrows represents a loop current. The total current in any given component is the sum (watch the directions!) of the individual loop currents that pass through that component. So, for example, the current through the 3 Ohm resistor would be I3, while the current through the 5 Ohm resistor would be I3 - I2 flowing from the center node to the junction with the 3 and 2 Ohm resistors.

I'll start you off by writing the equation for loop 1. The main loop current here is i1 which flows through all of the components in the loop, while the 6 Ohm resistor also carries i2, and the 8 Ohm resistor also carries i4. So, equating the voltage rise due to the 1V supply in the loop to the sum of the voltage drops across the resistors,

1V = 1Ω*i1 + 6Ω*(i1 - i2) + 8Ω*(i1 - i4)

and rearranging to separate the currents:

1V = i1*(1 + 6 + 8)Ω - i2*6Ω - i4*8Ω

Once you've written the equations for the other three loops, solve for i1 through i4. Then using these loop currents, find the individual currents in the components.

 

[mopar969]

Loop 2: 2v=(2+5+6)I2-6I1-5I3
Loop 3:3v=(3+5+7)I3-5I2-7I4
Loop 4:(4+8+7)I4-8I1-7I3

I wanted to check and see if these were correct before I continue?

 

[gneill]

Loop 2: 2v=(2+5+6)I2-6I1-5I3
Loop 3:3v=(3+5+7)I3-5I2-7I4
Loop 4:(4+8+7)I4-8I1-7I3

I wanted to check and see if these were correct before I continue?

Yes, that's fine, but don't forget the voltage in Loop 4.

 

[mopar969]

Oops sorry the voltage for loop 4 is 4 but I do not see how to solve for I1 through I4 using these loops?

 

[gneill]

Oops sorry the voltage for loop 4 is 4 but I do not see how to solve for I1 through I4 using these loops?

Four equations in four unknowns. You must have solved simultaneous equations before?

 

[mopar969]

I couldn't figure the problem out with substitutions so I set up a matrix and got 1 amp for all four currents is this correct? Also this would mean that there would be zero current through the 5, 6, 7, and 8 ohm resistors. Please explain how this would be possible?

 

[gneill]

I couldn't figure the problem out with substitutions so I set up a matrix and got 1 amp for all four currents is this correct? Also this would mean that there would be zero current through the 5, 6, 7, and 8 ohm resistors. Please explain how this would be possible?

Yes, 1 amp for each of the loop currents is correct, and yes, zero current in the inner resistors is correct. It's possible because there is no potential difference driving current though them; the circuit just happens to be balanced that way. Remember, zero is a perfectly good number, too!

 

[mopar969]

I am just a little confused by what you meant by their is no potential difference. Can you expand on why this makes on current on the inner resistors?

 

[gneill]

If it so happens that the potential at each corner of the outer loop is the same, then there will be no potential difference between any pair of them to drive current through the inner resistors.

Pick a corner node as a point of reference. Using the loop currents that you calculated (each is 1 amp; pay attention to its direction) calculate the voltage at the adjacent corners with respect to your reference node.