Solving for Spherical Coordinate Angles in 3D: Understanding the Formulas

In summary, the conversation is about learning about spherical angles in 3 dimensions and understanding the formula for calculating forces in the x, y, and z axes. The person also mentions a desire to upload pictures and asks for clarification on why there are different functions used in the equations for each axis. Another person suggests looking for a visual explanation online and provides a diagram. The original person expresses gratitude for the help.
  • #1
ricky_fusion
27
0
Hi guys,
This is my first time in this forum, thanks for your time.
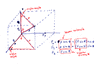
Now, I learn about spherical angles (vektor) in 3 Dimension
I still confuse about the formula, such as:
Fx = F sinφ cosθ ( in X axis = i)
Fy = F sinφ sinθ ( in y-axis = j)
Fz = F cosφ ( in z axis = k)

I want to send the pictures too, but I still don't have the way to upload it.Maybe next time.
Does anybody know about why in X axis there are sin and cos but in Z axis there is only cos??
Thaks for your help.
 
Mathematics news on Phys.org
  • #2
You can calculate all these by playing around with right triangles... I only just learned this stuff 2 weeks ago, so I can hardly explain it in words. I would look around online for a detailed picture that explains how the equations are geometrically derived. it isn't too complicated.
 
  • #3
Does this diagram help?
 

Attachments

  • spherical-coords.gif
    spherical-coords.gif
    30.1 KB · Views: 636
  • #4
Hmm..
Yes, you are right, Thanks alot.
 

FAQ: Solving for Spherical Coordinate Angles in 3D: Understanding the Formulas

What are spherical coordinate angles?

Spherical coordinate angles are a set of three angles used to specify the position of a point in three-dimensional space. They are commonly used in mathematical and scientific applications to describe the location of objects in spherical coordinates.

What are the three angles used in spherical coordinates?

The three angles used in spherical coordinates are the azimuth angle, the elevation angle, and the radius angle. The azimuth angle is measured from the positive x-axis, the elevation angle is measured from the positive z-axis, and the radius angle is the distance from the origin to the point.

How are spherical coordinate angles different from cartesian coordinates?

Spherical coordinates differ from cartesian coordinates in that they use angles to specify the position of a point, rather than just coordinates. This allows for a more natural representation of points on a sphere or other curved surfaces.

What is the range of values for spherical coordinate angles?

The azimuth and elevation angles both have a range of 0 to 360 degrees, while the radius angle has a range of 0 to infinity. However, in some cases, the azimuth angle may be limited to a range of -180 to 180 degrees.

What are some real-world applications of spherical coordinate angles?

Spherical coordinate angles are used in a variety of fields, including astronomy, physics, and engineering. They are used to describe the positions of celestial objects in the sky, the orientation of objects in 3D space, and the location of points on Earth's surface using latitude and longitude.

Similar threads

Why is ##x = r \sin{\phi} \cos{\theta}## in spherical coordinates?
Replies
26
Views
3K
Obtaining spherical coordinates by rotations
Replies
4
Views
1K
Coordinate transformation from spherical to rectangular
Replies
14
Views
2K
B Method of images and spherical coordinates
Replies
4
Views
1K
MHB Formula for changing a plane intersection angle
Replies
3
Views
2K
MHB Finding exact 3d coordinates in a falling pipe system with corners
Replies
20
Views
4K
I Orthogonal 3D Basis Functions in Spherical Coordinates
Replies
3
Views
3K
B Compound Angle Formula: Solving Double Angle Equations
Replies
5
Views
1K
Infinitesimal displacement in spherical coordinates
Replies
3
Views
3K
Proving a form ##z=f(r)## to be a surface of revolution
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top