- #1
AcousticBruce
- 37
- 0
How do I get to this equation?
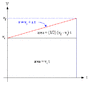
[tex]t=\frac{v_f-v_i}{a}[/tex]
Getting there from this equation is easy because there is only one t.
[tex]v_i=v_f+at[/tex]
But how do I get to it from this one?
[tex]s = v_it+\frac{1}{2}at^2[/tex]
Can someone help me with the steps. I am thrown off because there is multiple t's in the equations.
[tex]t=\frac{v_f-v_i}{a}[/tex]
Getting there from this equation is easy because there is only one t.
[tex]v_i=v_f+at[/tex]
But how do I get to it from this one?
[tex]s = v_it+\frac{1}{2}at^2[/tex]
Can someone help me with the steps. I am thrown off because there is multiple t's in the equations.