- #1
Tensaiga
- 43
- 0
i drew a digram for the forces and i found out the equations for accerleration... then I'm stuck...
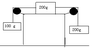
Question: Determine the tension in the strings, the acceleration, and how far the masses will go in 2.0s. (See attachement)
Well i drew a FBD, ,and i got three eqations for accerleration:
for mass 1 (100g):
A = (T2 - M1*G)/(M1)
A = (T2 - 0.1*9.8)/(0.1)
mass 2: (200g, on the floor)
A = (T1 - T2)/(M2)
A = (T1 - T2)/(0.2)
mass 3: (200g, going down on the right)
A = (M3*G - T1)/(M3)
A = (0.2*9.8 - T1)/(0.2)
Then what should i do after this? i can't equate 3 equations at once... can i?
Question: Determine the tension in the strings, the acceleration, and how far the masses will go in 2.0s. (See attachement)
Well i drew a FBD, ,and i got three eqations for accerleration:
for mass 1 (100g):
A = (T2 - M1*G)/(M1)
A = (T2 - 0.1*9.8)/(0.1)
mass 2: (200g, on the floor)
A = (T1 - T2)/(M2)
A = (T1 - T2)/(0.2)
mass 3: (200g, going down on the right)
A = (M3*G - T1)/(M3)
A = (0.2*9.8 - T1)/(0.2)
Then what should i do after this? i can't equate 3 equations at once... can i?