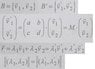Solving Matrix Basis Problem with Orthogonal Matrix B | Need Help Urgently

In summary, the conversation discusses a homework problem involving two basis and an orthogonal matrix. The goal is to prove that the lambdas in the problem are equal. However, the conversation also suggests that the lambdas will only be equal if the two basis are the same, and the use of vector norm and inner product may be necessary to solve the problem.
  • #1
Lindsayyyy
219
0
Hi everyone

Homework Statement



File at attachment. Given are two basis and the orthogonal matrix B. When r=...(see attachment) I shall proof that the lambdas are equal.

Homework Equations



-

The Attempt at a Solution



I have much trouble with this exercise and it is quite urgent. I tried to express v1' via v1 and v2, but this doesn't bring me to the solution, for example I have: v1' = av1 + bv2 etc.

Can anyone help me with this?

Thanks for the help in advance
 

Attachments

  • MATHS.JPG
    MATHS.JPG
    7.1 KB · Views: 470
Physics news on Phys.org
  • #2
Hi Lindsayyyy! :smile:

I don't really get your problem statement.

Any vector r can be represented uniquely with respect to a basis.
With respect to a different basis the representation is again unique, but will always be different.
So as I understand your problem, you can only proof that the lambdas are different.

The lambdas will only be the same iff the 2 basis are the same (that is, if M is the identity matrix).So I suspect you're not supposed to proof the lambdas are the same.
Especially seeing the last equation saying something about what appears to be the vector norm of an inner product of the lambdas.
Still not quite sure what it says though. Can you clarify?

I can say that vector norm and inner product are preserved by an orthogonal matrix, so you probably need to do something with that.
 
Last edited:

FAQ: Solving Matrix Basis Problem with Orthogonal Matrix B | Need Help Urgently

What is a matrix?

A matrix is a rectangular array of numbers or symbols that can be used to represent mathematical or logical data. It is made up of rows and columns, and is often used in linear algebra to solve equations and represent transformations.

What is a basis?

In linear algebra, a basis is a set of linearly independent vectors that span a vector space. This means that any vector in the space can be written as a linear combination of the basis vectors. A basis is often used to find solutions to systems of equations and to represent transformations.

What is the basis problem?

The basis problem is the task of finding a set of basis vectors for a given vector space. This can involve determining if a set of vectors is linearly independent or finding a minimal set of vectors that span the space. In some cases, the basis problem may also involve finding a basis for a specific subspace within a larger vector space.

How is the basis problem related to the matrix problem?

The basis problem and the matrix problem are closely related because matrices can be used to represent linear transformations and solve systems of equations. In solving the basis problem, one may need to use matrices to find a basis for a vector space or a subspace. In turn, solving the matrix problem may involve finding a basis for the solution space of a particular equation.

Why is the basis problem important in mathematics?

The basis problem is important in mathematics because it is fundamental to many areas of study, including linear algebra, differential equations, and abstract algebra. It allows for the efficient and accurate representation and solution of complex mathematical problems, and is essential for understanding and applying a wide range of mathematical concepts and techniques.

Similar threads

Proving Linear Independence of Av1, ..., Avk and Conditions for Basis in Rm
Replies
17
Views
2K
Left and right inverses of a non-square matrix
Replies
7
Views
2K
Question about linear transformations
Replies
3
Views
1K
Coefficients that make Gaussian elimination impossible?
Replies
5
Views
2K
Changing Basis: Matrix E->F vs. Matrix B->C
Replies
15
Views
2K
I Proof that if T is Hermitian, eigenvectors form an orthonormal basis
Replies
3
Views
2K
Give a 2x2 matrix with Det(A)=+/-1 that is not orthogonal.
Replies
10
Views
8K
Prove 3x3 Skew symmetric matrix determinant is equal to zero
Replies
5
Views
5K
Matrix of rotated elements (stiffness matrix)
Replies
2
Views
2K
Eigenvalues of an orthogonal matrix
Replies
18
Views
3K

Hot Threads

Recent Insights

Back
Top