The distribution of function of random variable

In summary, the conversation revolves around finding the distribution of a variable, y, based on the distribution of another variable, x. The speaker mentions finding the density of x using a Bernoulli trial and creating a staircase plot. They also mention referencing a solution in a book, which uses equal probabilities for heads and tails. The conversation ends with a question about determining the fairness of a coin based on the results of a series of tosses.
  • #1
ecesiu
7
0
i have this question
image.png

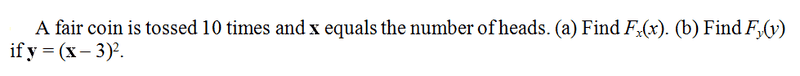
i do find the distribution like this figure :
dis.png

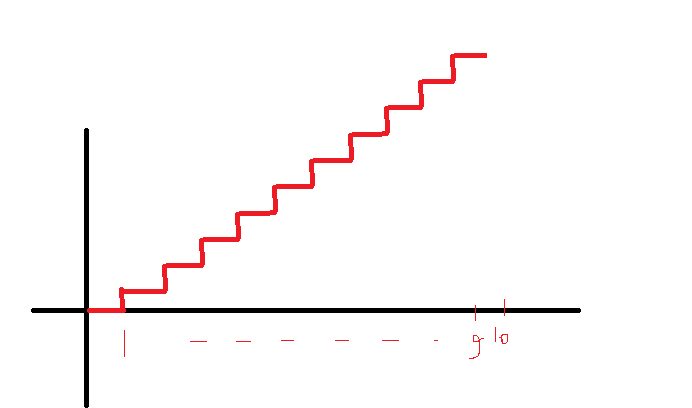
and i plot the y like this:
g_x.png

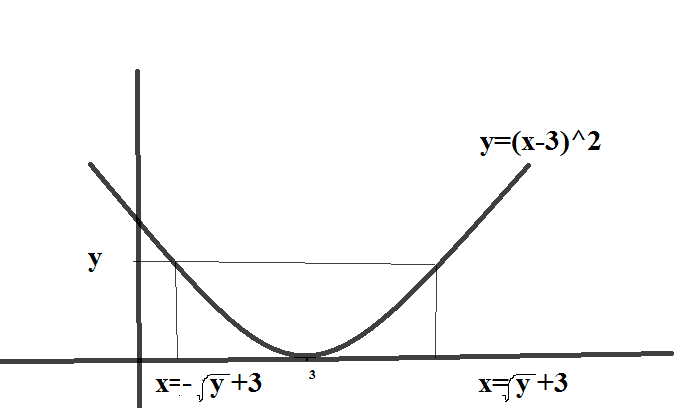
now i want to find the distribution of y
i tried to take the distribution for each interval in Fx(x) like this :
image.png

but the solution in the book said :
image.png

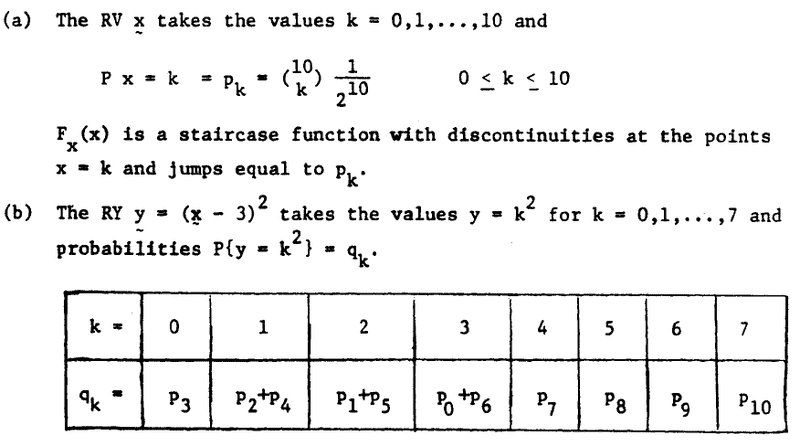
who is wrong me or the book please help
 
Physics news on Phys.org
  • #2
Hey ecesiu and welcome to the forums.

You missed out giving us any of the information.
 
  • #3
which information you mean?
 
  • #4
Like the solution the book gave, the distribution definition, all the other relevant information: stuff like that.
 
  • #5
firest i found the density of x which is Bernoulli trial :
PK=Cn(10,k) * p^k * q^(10-k) , k= 0,1,...,10
the distribution is a staircase of the density
which i sketch , the book solution is here :
image.png
 
  • #6
p=q=0.5 because the coin is fair
where p is the probability of getting head , q is the probability of getting tail
 
  • #7
So what are you trying to do? Are you trying to figure out whether you think a coin is fair given a number of tosses for heads and tails?
 

FAQ: The distribution of function of random variable

What is a random variable?

A random variable is a variable whose value is uncertain or random. In other words, it can take on different values with varying probabilities. It is often denoted by the capital letter X.

What is the distribution of a random variable?

The distribution of a random variable refers to the set of possible values it can take on and the corresponding probabilities of each value occurring. It can be represented through a histogram, probability mass function, or cumulative distribution function.

How is the distribution of a random variable determined?

The distribution of a random variable is determined by its underlying probability distribution. This can be a discrete distribution, such as a binomial or Poisson distribution, or a continuous distribution, such as a normal or exponential distribution.

Why is understanding the distribution of a random variable important?

Understanding the distribution of a random variable is important because it allows us to make predictions and draw conclusions about the likelihood of certain outcomes. It also helps us to calculate probabilities and make informed decisions in various fields, such as finance, engineering, and social sciences.

Can the distribution of a random variable change?

Yes, the distribution of a random variable can change if the underlying circumstances or parameters change. For example, if the probability of success in a binomial distribution changes, the distribution of the corresponding random variable will also change.

Similar threads

I Linear regression and random variables
Replies
30
Views
3K
I How to show these random variables are independent?
Replies
1
Views
566
I Sampling theory and random sample
Replies
5
Views
2K
I Relating Moments from one Distribution to the Moments of Another
Replies
7
Views
2K
MHB Distribution and Density functions of maximum of random variables
Replies
6
Views
4K
I Statistical modeling and relationship between random variables
Replies
7
Views
2K
I Failure rate for a uniformly distributed variable
Replies
3
Views
2K
I On transformation of r.v.s. and sigma-finite measures
Replies
1
Views
834
A How Is the CDF Expressed for a Uniform Distribution on a Circle?
Replies
8
Views
1K
I Distribution of Sum of Two Weird Random Variables....
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top