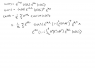- #1
aaaa202
- 1,169
- 2
Homework Statement
I am supposed to show equation 6.6 on page 97 of http://www.phys.lsu.edu/~jarrell/CO...hysics Henrik Bruus and Karsten Flensberg.pdf
I have tried to plug A and the expression for ln(t)> into 6.3 a) on page 96 but end up with a double integral after doing the linear approximation of the time evolution operator. Is my method correct and if so, how do I conjugate transpose the expression for U when given by the first order integral? Second of all I am quite confused by the notation <A>_0. Does that simply mean <A(t0)> or am I missing something?
Homework Equations
The Attempt at a Solution
I have attached my attempt.