Time it takes for stacked boxes to cover distance

[Jonathan1515]

Homework Statement

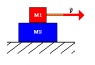
he coefficient of static friction is 0.682 between the two blocks shown. The coefficient of kinetic friction between the lower block and the floor is 0.119. Force F causes both blocks to cross a distance of 6.95 m, starting from rest. What is the least amount of time in which the motion can be completed without the top block sliding on the lower block, if the mass of the lower block is 1.64 kg and the mass of the upper block is 2.41 kg?

Homework Equations

Fk=\muN
Fs(max)=\muN

The Attempt at a Solution

First I found the max static friction which was 16.107N.
Then I found the kinetic friction which was 4.723N.
First I tried to just subtract the static from kinetic, and then use that as the pushing force, which resulted in a=2.81m/s/s but when I used that acceleration in kinematics equation I did not get the correct answer (i got 2.22s, I don't know what the correct answer is)

I also then saw this thread and tried the method.https://www.physicsforums.com/showthread.php?t=533845"
I split it into the two masses on a string as described, but I got confused at what to do when concentrating on m1. Would this method be what I need to use, or is there another way I can solve this problem.

 

[PhanthomJay]

Try drawing free body diagrams. Look at the top block, identify all the forces acting in the x direction, and use Newton's 2nd law in that direction to get an equation. Then look at the bottom block, identify all forces acting on it in the x direction, and use Newton's 2nd law in that direction on this block, to get a second equation.

 

[Jonathan1515]

Ok I got two equations:
m2a= Fs - Fk
m1a= F - Fs

a must be equal in both, so I set both equal in terms of a, and then solved for F which I don't know.

I got an answer for F of 32.83N, which I then used to derive an acceleration of 8.106m/s/s. This seems to be very big. Does it look like I've done the right thing or did I make a mistake?

 

[PhanthomJay]

You didn't attach a sketch, is m2 is the heavier block on top, and m1 is on the bottom, and is the Force F applied to the top or bottom block?? Please clarify.

 

[gneill]

Hi Jonathan1515, welcome to Physics Forums.

You can solve the problem by consideration of the Free Body Diagrams for each block, of course. The method of redrawing the problem as two separate blocks connected by a string is merely a device to highlight the individual forces that are acting on each block.

You might want to post the diagram that accompanies your problem so that we can see where the forces are acting. In particular, where and how is the pushing force being applied? Can you write an equation for the acceleration of the pair of blocks given the applied force (and assuming that no slipping is taking place)?

 

[Jonathan1515]

Sorry, here's the picture of the problem.

M2 is the light block and is on the bottom.
M1 is the heavier block, and on top, and this is the one that is being pulled.

So do my previous equations make sense.

m2a= Fs - Fk
m1a= F - Fs

a must be equal in both, so I set both equal in terms of a, and then solved for F which I don't know.

I got an answer for F of 32.83N, which I then used to derive an acceleration of 8.106m/s/s. This seems to be very big. Does it look like I've done the right thing or did I make a mistake?

Cause I tried it with that value of acceleration and was unable to get the correct answer.
I'm not entirely sure where I've gone wrong with the equations that I got from my FBD, and I've tried to look at the problem many different ways, but I can never get the right answer.

 

[gneill]

In this problem the idea is to find the maximum allowable acceleration (you then use that to find the minimum time to cover the given distance). If you concentrate on block M2 of your diagram you can write an expression for that maximal acceleration from the forces that can act on it. In fact you've already done this above! m2*a = Fs - Fk. So what's the acceleration?

 

[Jonathan1515]

ok so that means a=6.94m/s/s, and therefore the equation d=0.5a t^2 becomes 6.95= 3.47 t^2.
This solves for t=1.42s
Thanks, that ended up being the right answer. I think I may have done it before a similar way but inputted the wrong numbers by accident, so that's why I was confused.
Thank you very much, it made it seem much easier with your help, and now I'm done my assignment.

 

[PhanthomJay]

Sorry, here's the picture of the problem.

M2 is the light block and is on the bottom.
M1 is the heavier block, and on top, and this is the one that is being pulled.

So do my previous equations make sense.


Cause I tried it with that value of acceleration and was unable to get the correct answer.
I'm not entirely sure where I've gone wrong with the equations that I got from my FBD, and I've tried to look at the problem many different ways, but I can never get the right answer.

Your equations are correct, good work, but i get a slightly different number. Maybe you have a math error or you didn't calculate your variables correctly. You can always check your results by using a free body diagram of the system , F - Fk = (M1 + M2)a