- #1
ProPM
- 66
- 0
Hi,
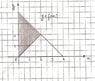
I have a graph of a function, but it has no specific equation, just a drawing, denoted by f(x). The question asks me to do the 1/f(x) of that graph. What does that mean?
Thanks in advance.
I have a graph of a function, but it has no specific equation, just a drawing, denoted by f(x). The question asks me to do the 1/f(x) of that graph. What does that mean?
Thanks in advance.