- #1
LearninDaMath
- 295
- 0
My teacher writes 3 dimensions like this:
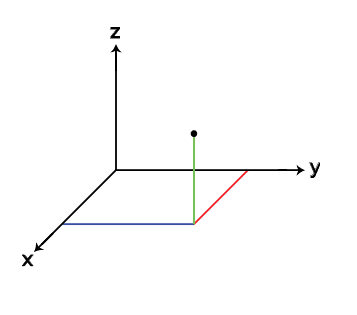
My textbook writes it like this:
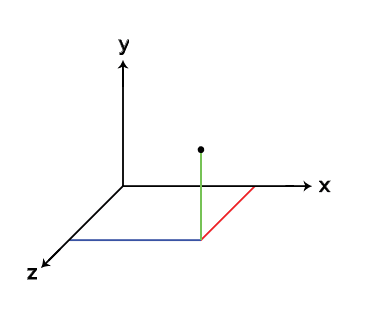
If my online H/W is not directly written by my teacher and not directly written by my textbook (MasteringPhysics online HW), then when presented with a vector such as:
A = (2,1,-4)
Should I read it as:
A = (2x, 1y, -4z) or A = (2z, 1x, -4y)
I'm going to guess the H/W is more in line with the teacher's convention than my textbook's convention and that's how I'm going to proceed. However, if anyone has more insightful input as to how to read this vector, I'm all ears.
My textbook writes it like this:
If my online H/W is not directly written by my teacher and not directly written by my textbook (MasteringPhysics online HW), then when presented with a vector such as:
A = (2,1,-4)
Should I read it as:
A = (2x, 1y, -4z) or A = (2z, 1x, -4y)
I'm going to guess the H/W is more in line with the teacher's convention than my textbook's convention and that's how I'm going to proceed. However, if anyone has more insightful input as to how to read this vector, I'm all ears.