- #1
Saitama
- 4,243
- 93
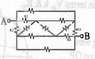
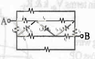
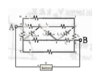
Homework Statement
http://i50.tinypic.com/w0ggl.png
Homework Equations
The Attempt at a Solution
I am stuck at part (a) (i haven't yet tried the part (b)).
I really have no clue on how should i go on finding the equivalent resistance, i don't see a way to reduce it to simpler parallel and series combinations. Any help is appreciated.