What is the Limit of f(x) as x Approaches Zero in the Interval [-1,1]?

[daytrader]

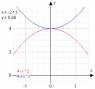
if 4-x^2 < f(x) < 4 + x^2 for x in [-1,1] then what's lim as x goes to zero of f(x) ...

this setup looks like epsilon form .. not sure how to interpret this guy...

 

[bartek2009]

Is it not just 4? Since f(x) is bounded by the two curves (see picture attached).

---

 

[daytrader]

double checked it. the have it right. any ideas?

 

[HallsofIvy]

Ideas about what? You have already been told that the limit is 4. That should be obvious from the "sandwiching" property. f(x) is always between 4- x² and 4+ x² and they both go to 4.

 

[daytrader]

may be I don't understand the problem to begin with.. can you explain. thanks

 

[snipez90]

Just think of it intuitively. What happens to the given bounds on f as x gets smaller and smaller (approaching zero)? Don't worry about any particular theorems, if you don't understand what is going on here you need to revisit the intuitive concept of a limit.