What Is the Maximum Coefficient of Static Friction for a Sliding Block System?

In summary, the conversation is about finding the maximum value for the coefficient of static friction between two blocks connected by a massless rope on a frictionless pulley. Through a series of calculations and discussions, the correct value is determined to be 0.573.
  • #1
yuvlevental
44
0

Homework Statement


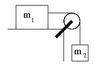
A 5.50 kg block (m1) is connected by means of a massless rope to a 3.15 kg block (m2). The pulley is frictionless. Calculate the maximum value for the coefficient of static friction, if the 5.50 kg block is to begin sliding.

The diagram is attatched to the post.

Homework Equations


Friction coefficient = (Frictional Force)/(Normal Force)
Acceleration = (m2*9.8)/(m1 + m2)
Of course, Force = mass*acceleration

The Attempt at a Solution


Acceleration = (m2*9.8)/(m1 + m2)
Acceleration = 3.5688 m/s^2
3.5688*5.5 = 19.6284 N = frictional force
Normal force = 5.5*9.8 = 53.9 N

19.6284/53.9 = .36416

I know that the answer isn't right, what am I doing wrong?
 

Attachments

  • tablepulley.gif
    tablepulley.gif
    776 bytes · Views: 499
Last edited:
Physics news on Phys.org
  • #2
Attach the diagram as an image. (That site requires authorization to view.)
 
  • #3
Ok, I did.
 
  • #4
Note that the block is just about to barely begin sliding. So what can you take as the acceleration? (Hint: Note that you are finding the coefficient of static friction.)
 
  • #5
I already gave the acceleration, 3.5688 m/s^2, and doesn't the force of static friction balance the force of tension, which is 3.5688*5.5?
 
  • #6
yuvlevental said:
I already gave the acceleration, 3.5688 m/s^2,
I know. My point was that this acceleration is wrong. :wink: How did you arrive at this value?
and doesn't the force of static friction balance the force of tension,
Exactly! So what's the acceleration if the forces are balanced?
 
  • #7
The weight of the hanging mass exerts a net force on both masses. (Assuming that the surface is frictionless)

(3.15*9.8)/(3.15+5.5) = 3.5688 m/s^2

Also, the acceleration needs to be zero, so then i did 5.5*3.5688 to find the frictional force.
 
Last edited:
  • #8
yuvlevental said:
The weight of the hanging mass exerts a net force on both masses. (Assuming that the surface is frictionless)

(3.15*9.8)/(3.15+5.5) = 3.5688 m/s^2
You found the acceleration of the masses assuming no friction. But you know there's friction, so this is not relevant.

Also, the acceleration needs to be zero
Doesn't this contradict what you just did above?

The acceleration is zero. So what's the net force on m1?
 
  • #9
there is none because force is equal to mass * acceleration. so then what am i doing wrong?
 
  • #10
The net force is zero. So add up the forces on m1 and set equal to zero. What horizontal forces act on m1?

(This is a static equalibrium problem.)
 
  • #11
Ok, I got it right...

I figured that the tension in the rope would be equal to the weight of m2 in equilibrium.
Then, I set it to equal the force of friction.
I divided the force of friction by the mass of m1 to get .573.

Thanks for the help!
 
  • #12
Good! You're welcome.
 

FAQ: What Is the Maximum Coefficient of Static Friction for a Sliding Block System?

How does a sliding block and pulley system work?

A sliding block and pulley system is a mechanical device that uses a combination of a block and a pulley to transfer force and motion. The block is a solid object with a smooth surface that can slide along a flat surface. The pulley is a simple machine that consists of a wheel with a groove around its circumference. When a force is applied to the block, it moves along the flat surface, and the pulley helps to change the direction of the force, making the movement easier.

What are the main components of a sliding block and pulley system?

The main components of a sliding block and pulley system are the block, the pulley, and the rope or wire that connects them. The block can come in various shapes and sizes, but it always has a smooth surface to facilitate sliding. The pulley is usually made of metal or plastic and has a groove around its circumference to hold the rope or wire. The rope or wire plays a vital role in connecting the block and pulley and transmitting force and motion between them.

What are the advantages of using a sliding block and pulley system?

There are several advantages to using a sliding block and pulley system. Firstly, it can change the direction of the applied force, making it easier to move an object in a different direction. Secondly, it can reduce the amount of force needed to move an object, making it useful for lifting heavy objects. Additionally, a sliding block and pulley system can also provide a mechanical advantage, meaning that the output force is greater than the input force, making it a useful tool for many tasks.

What are some real-world applications of sliding block and pulley systems?

Sliding block and pulley systems have various applications in the real world. They are commonly used in construction and engineering for lifting heavy objects such as building materials. They are also used in elevators to lift and lower the elevator car. In transportation, they are used in vehicles such as cranes and forklifts. Additionally, they are used in household items such as window blinds, curtains, and garage doors.

Are there any limitations to using a sliding block and pulley system?

Like any mechanical system, there are limitations to using sliding block and pulley systems. One of the main limitations is friction, which can reduce the efficiency and effectiveness of the system. Another limitation is the weight limit of the system, as it can only handle a certain amount of weight before becoming unstable. Additionally, the length and quality of the rope or wire used can also affect the performance of the system. Regular maintenance and proper use can help to minimize these limitations.

Similar threads

Find the acceleration of the system (2 blocks sliding on a table)
Replies
23
Views
2K
Newton's Second Law (Pulley Sustem)
Replies
3
Views
1K
Friction, Mass and Acceleration: Analyzing Block Motion
Replies
6
Views
2K
Calculating Net Force of 3 Blocks in an Elevator
Replies
9
Views
2K
Static Friction Required to Keep the System from Moving (Two Boxes)
Replies
16
Views
2K
Two blocks, a fixed pulley and friction
Replies
4
Views
2K
Newton's law problem: Pushing 2 stacked blocks on a horizontal table
Replies
13
Views
2K
Finding the work done by a block
Replies
4
Views
2K
When Friction the block m2 start to move?
Replies
11
Views
2K
Forces/Dynamics: A block sliding on a plate
2
Replies
45
Views
6K

Hot Threads

Recent Insights

Back
Top