Where will the normal force on the block act if it tips?

[Bearbull24.5]

Homework Statement

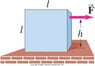
A cube of side l rests on a rough floor. It is subjected to a steady horizontal pull F, exerted a distance h above the floor as shown below. As F increases, the block will either begin to slide, or begin to tip over and thus rotate. Determine the coefficient of static friction so that (a) the block begins to slide rather than tip; (b) the block begins to tip. [Hint: Where will the normal force on the block act if it tips?]

Homework Equations

fs=(u(s))(N)

The Attempt at a Solution

I'm not even sure where to start this problem. With no values the equation for the coefficient of static friction seems useless.

 

[radou]

Set the sum of moments around the point of rotation of the block equal to zero. You can get the mass of the block out of this equation. Now you have everything you need to calculate the coefficient of friction.

 

[AdmiralR]

Set the sum of moments around the point of rotation of the block equal to zero. You can get the mass of the block out of this equation. Now you have everything you need to calculate the coefficient of friction.

Could you explain further?
I have the equations
f_s=u_s * n
|n|=mg
f_s=u_s*m*g

I=mr^2
m=(r^2)/I

I don't understand how setting
summation(mr^2)=0 will help me.

I'm also assuming that the "point of rotation" is just the edge of the cube.