- #1
VortexLattice
- 146
- 0
Hi all,
I'm doing a practice problem and I thought I had a good solution, but it turns out I'm wrong and I'd like to know exactly why. The book seems to do it in different way, but I don't see why theirs is the right way.
The problem is this:

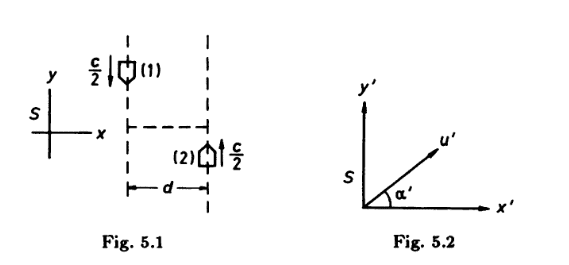
So, here's the process I tried doing:
-Find what the y component of the package velocity with respect to S1 (S1 is rocket 1's frame), using the velocity addition rule since we have the velocity of S with respect to S1 and the velocity of the package with respect to S
-Find the velocity of rocket 2 with respect to S1, using the velocity addition rule since we have the velocity of S with respect to S1 and the velocity of rocket 2 with respect to S
-Then, to make it so the package hits rocket 2 as it goes across the gap, we set these two velocities equal.
This is where the solution and I seem to disagree, the solution says that the y component of the package velocity and the velocity of rocket 2 should match in frame S, not rocket 1's frame! I guess I don't actually see why one is preferable over the other, but theirs must be right. If I had to guess I'd say it's something involving proper time or proper velocity, but I don't see what exactly.
Any help would be great, thanks!
I'm doing a practice problem and I thought I had a good solution, but it turns out I'm wrong and I'd like to know exactly why. The book seems to do it in different way, but I don't see why theirs is the right way.
The problem is this:
So, here's the process I tried doing:
-Find what the y component of the package velocity with respect to S1 (S1 is rocket 1's frame), using the velocity addition rule since we have the velocity of S with respect to S1 and the velocity of the package with respect to S
-Find the velocity of rocket 2 with respect to S1, using the velocity addition rule since we have the velocity of S with respect to S1 and the velocity of rocket 2 with respect to S
-Then, to make it so the package hits rocket 2 as it goes across the gap, we set these two velocities equal.
This is where the solution and I seem to disagree, the solution says that the y component of the package velocity and the velocity of rocket 2 should match in frame S, not rocket 1's frame! I guess I don't actually see why one is preferable over the other, but theirs must be right. If I had to guess I'd say it's something involving proper time or proper velocity, but I don't see what exactly.
Any help would be great, thanks!