- #1
hellophyscis
- 1
- 0
Given in my book-
1."Velocity Of approach - It is the rate at which distance between two moving particle decreases.
V(Approach) =V1cosα + V2cosβ "
2."When the distance between two particles is minimum, the relative veloctiy of approcah is 0"
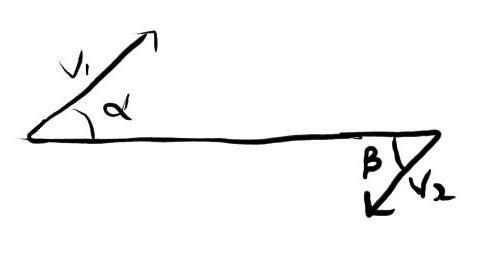
3."V1cosα + V2cosβ = 0 ...when distance is minimum(diagram in attachment below)"
Please Explain Why?
And, the above equation will become 0 only if cosα = 0 and cosβ = 0 at same time, but if α and β are not equal, then cosα and cosβ cannot be 0 at same time. Thus the Equation is worng but giving correct answers.
Please Explain Why?
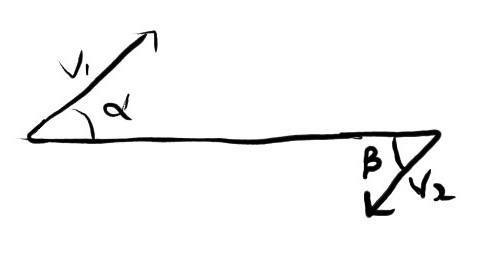
1."Velocity Of approach - It is the rate at which distance between two moving particle decreases.
V(Approach) =V1cosα + V2cosβ "
2."When the distance between two particles is minimum, the relative veloctiy of approcah is 0"
3."V1cosα + V2cosβ = 0 ...when distance is minimum(diagram in attachment below)"
Please Explain Why?
And, the above equation will become 0 only if cosα = 0 and cosβ = 0 at same time, but if α and β are not equal, then cosα and cosβ cannot be 0 at same time. Thus the Equation is worng but giving correct answers.
Please Explain Why?