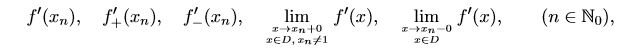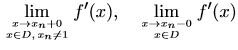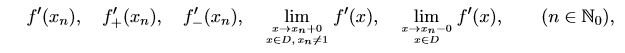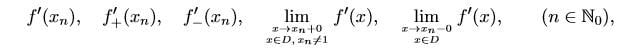- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
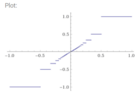
Let $f:[-1,1]\rightarrow \mathbb{R}$ be defined by \begin{equation*}f(x)=\begin{cases}\frac{1}{k} & \text{ for } x\in \left (\frac{1}{k+1}, \frac{1}{k}\right ], \ k \in \mathbb{N}\\ 0 & \text{ for } x=x_0=0 \\ \frac{1}{k} & \text{ for } x\in \left [\frac{1}{k}, \frac{1}{k-1}\right ), \ k \in \mathbb{Z}\setminus \mathbb{N}_0, \ \text{ i.e. } (-k)\in \mathbb{N}\end{cases}\end{equation*}
Let $f:[-1,1]\rightarrow \mathbb{R}$ be defined by \begin{equation*}f(x)=\begin{cases}\frac{1}{k} & \text{ for } x\in \left (\frac{1}{k+1}, \frac{1}{k}\right ], \ k \in \mathbb{N}\\ 0 & \text{ for } x=x_0=0 \\ \frac{1}{k} & \text{ for } x\in \left [\frac{1}{k}, \frac{1}{k-1}\right ), \ k \in \mathbb{Z}\setminus \mathbb{N}_0, \ \text{ i.e. } (-k)\in \mathbb{N}\end{cases}\end{equation*}
- Draw $f$
- Examine at the points $x_0=0$ and $x_n=\frac{1}{n}, n\in \mathbb{N}$, the existence of
View attachment 7648
where $D=\{x\in (-1,1): f'(x)\text{ exists }\}$. Calculate their values, if they exist.
- How could we draw that function?
Doesn't it depend on how we choose $k$ ?
(Wondering) - Do we not have to check first the existence of $f_+'(x_n)$ and $f_-'(x_n)$ and then it follows if $f'(x_n)$ exist?
We have that $$f_+'(x_n)=\lim_{x\rightarrow x_n^+}\frac{f(x)-f(x_n)}{x-x_n}=\lim_{x\rightarrow \frac{1}{n}^+}\frac{f(x)-\frac{1}{n}}{x-\frac{1}{n}}$$ Does it holds that $\displaystyle{\lim_{x\rightarrow x_n^+}f(x)=\frac{1}{n}}$ ? (Wondering)