Recent content by phyTens
-
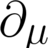
I How is there any pressure at all in isotropic radiation?
Thank you for all the answers! I think I understand this much better now. The idea that a particle moving in the opposite direction has negative momentum, has particularly helped.- phyTens
- Post #10
- Forum: Astronomy and Astrophysics
-
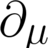
I How is there any pressure at all in isotropic radiation?
I understand your explanations (that pressure can be interpreted as hollowing a cavity of some sort and see what force is being applied by the gas), and I would totally agree with you if it weren't for the derivation of the pressure in the aforementioned book: ------------ The pressure of the...- phyTens
- Post #6
- Forum: Astronomy and Astrophysics
-
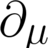
I How is there any pressure at all in isotropic radiation?
It is a standard result that in a blackbody radiation there is a pressure (at a certain frequency), given by $$P_\nu=\frac 1 3 U_\nu$$ However, I am quite confused by this result. Firstly, how do we even define pressure in radiation gas? I would think that this would be the pressure on a small...- phyTens
- Thread
- Blackbody radiation Radiation pressure
- Replies: 20
- Forum: Astronomy and Astrophysics
-
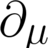
How to show that this expression with tensors reduces to zero?
Oh, thank you! I really wanted to use this fact, but I was worried because ##g## and ##h## also show up in the factor before the difference as well. Is this not a problem when cancelling out the terms in the difference?- phyTens
- Post #5
- Forum: Calculus and Beyond Homework Help
-
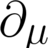
How to show that this expression with tensors reduces to zero?
I used this fact to derive the last expression in the post, but I haven't been able to go much further. Could you be more specific of where to apply this fact?- phyTens
- Post #3
- Forum: Calculus and Beyond Homework Help
-
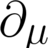
How to show that this expression with tensors reduces to zero?
I simply just wrote down the definition of ##\Gamma'^a_{bc}##, and inserted the transformations of ##g'^{ad}##, ##g'_{dc,b}##, and the like terms. After some rearranging and cancelling out, $$\Gamma'^a_{bc}=\frac{\partial x'^a}{\partial x^e}\frac{\partial x^f}{\partial x'^b}\frac{\partial...- phyTens
- Thread
- Expression Tensors Zero
- Replies: 6
- Forum: Calculus and Beyond Homework Help