- #1
snoopies622
- 846
- 28
Recently I read that from the perspective of a distant observer
[tex] (r \gg r_s =\frac{2GM}{c^2}) [/tex]
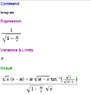
the speed of a beam of light moving directly towards the center of a spherical (non-rotating, non-charged) object decreases because if we set [tex] ds^2=d\theta ^2 =d\phi ^2 = 0 [/tex] then
[tex] \frac {dr}{dt}=c(1-\frac {r_s}{r}) [/tex].
I was wondering why this interpretation is favored over the following one: in the Schwarzschild metric, the speed of light stays the same everywhere, but the distance between successive r coordinates increases asympotically as [tex] r \rightarrow r_s [/tex]. This would also be consistent with
[tex] \frac {dr}{dt} \rightarrow 0[/tex] for light as [tex]r \rightarrow r_s[/tex].
Does this interpretation fail somehow?
[tex] (r \gg r_s =\frac{2GM}{c^2}) [/tex]
the speed of a beam of light moving directly towards the center of a spherical (non-rotating, non-charged) object decreases because if we set [tex] ds^2=d\theta ^2 =d\phi ^2 = 0 [/tex] then
[tex] \frac {dr}{dt}=c(1-\frac {r_s}{r}) [/tex].
I was wondering why this interpretation is favored over the following one: in the Schwarzschild metric, the speed of light stays the same everywhere, but the distance between successive r coordinates increases asympotically as [tex] r \rightarrow r_s [/tex]. This would also be consistent with
[tex] \frac {dr}{dt} \rightarrow 0[/tex] for light as [tex]r \rightarrow r_s[/tex].
Does this interpretation fail somehow?
 Orbiting satellites do seem to provide a big easy-to-observe natural clock for comparisons. Only trouble is, there are no natural stable orbits below the photon horizon , maybe slightly higher?
Orbiting satellites do seem to provide a big easy-to-observe natural clock for comparisons. Only trouble is, there are no natural stable orbits below the photon horizon , maybe slightly higher?