- #36
yuiop
- 3,962
- 20
Getting back to steve's original question:
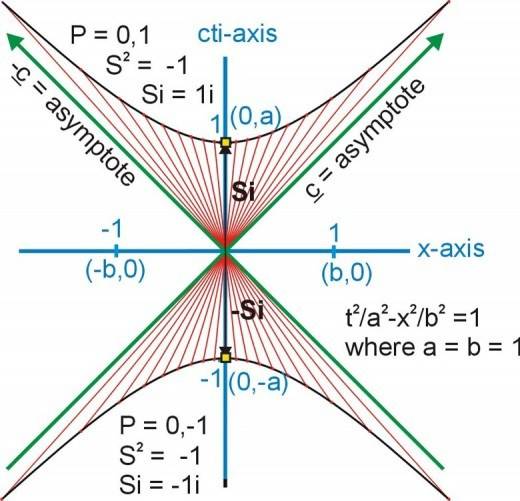
From the above image, you can see that:
[tex]t^2 - x^2 = constant =a^2 = (cdt^2) -dx^2[/tex]
Note that the constant is not necessarily one. The hyperbolic curve is the horizontal version that represents a curve of constant proper time for various relative velocites, rather than using the vertical version you were using before that represents a curve of constant proper disnance.
Now if we use the hyperbolic identity:
[tex] \cosh^2\phi - \sinh^2\phi = 1 [/tex]
we can say:
[tex] a^2(\cosh^2\phi- \sinh^2\phi) = (cdt)^2 - dx^2 [/tex]
[tex] \cosh^2\phi - \sinh^2\phi = \frac{(cdt)^2}{a^2} - \frac{dx^2}{a^2} [/tex]
From the above it natural to make the association:
[tex]\cosh^2 \phi = \frac{(cdt)^2}{a^2}[/tex]
[tex]\Rightarrow \cosh^2 \phi = \frac{(cdt)^2}{(cdt)^2 - dx^2} = \frac{1}{1-\beta^2} = \gamma^2[/tex]
and
[tex]\sinh^2 \phi = \frac{dx^2}{a^2}[/tex]
[tex]\Rightarrow \sinh^2 \phi = \frac{dx^2}{(cdt)^2 - dx^2} = \frac{\beta^2}{1-\beta^2} = \beta^2 \gamma^2[/tex]
If you look at the diagram below:
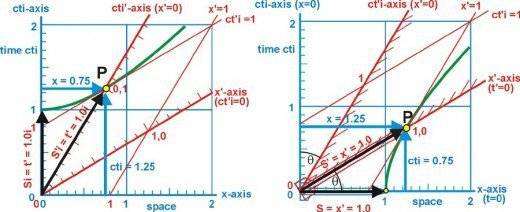
You can see that the x' axis has been rotated anticlockwise while the t' axis has been rotated clockwise relative to the x and t axes respectively. The amount of rotation of the axes depends on the relative velocity between the F and F' frames. The relative velocity in the above diagram is 0.6c so the proper time t' =1 translates to t=0.8 and the proper distance x' =1 translates to x=0.8. Note that point P = (x',t') = (0,1) remains on the horizontal hyperbola in the left diagram, for all relative velocities and the point P = (x',t') = 1,0) remains on the vertical hyperbola in the right diagram, for all relative velocities.
Diagrams from http://hubpages.com/hub/Minkowski-Diagram
stevmg said:I was trying to find the relationship between a and [tex]\phi[/tex].
I know that sinh [tex]\phi[/tex] = ct/a and cosh [tex]\phi[/tex] = x/a
...
...
Now I have to let the dust settle, have you all agree what I just wrote was correct...
From the above image, you can see that:
[tex]t^2 - x^2 = constant =a^2 = (cdt^2) -dx^2[/tex]
Note that the constant is not necessarily one. The hyperbolic curve is the horizontal version that represents a curve of constant proper time for various relative velocites, rather than using the vertical version you were using before that represents a curve of constant proper disnance.
Now if we use the hyperbolic identity:
[tex] \cosh^2\phi - \sinh^2\phi = 1 [/tex]
we can say:
[tex] a^2(\cosh^2\phi- \sinh^2\phi) = (cdt)^2 - dx^2 [/tex]
[tex] \cosh^2\phi - \sinh^2\phi = \frac{(cdt)^2}{a^2} - \frac{dx^2}{a^2} [/tex]
From the above it natural to make the association:
[tex]\cosh^2 \phi = \frac{(cdt)^2}{a^2}[/tex]
[tex]\Rightarrow \cosh^2 \phi = \frac{(cdt)^2}{(cdt)^2 - dx^2} = \frac{1}{1-\beta^2} = \gamma^2[/tex]
and
[tex]\sinh^2 \phi = \frac{dx^2}{a^2}[/tex]
[tex]\Rightarrow \sinh^2 \phi = \frac{dx^2}{(cdt)^2 - dx^2} = \frac{\beta^2}{1-\beta^2} = \beta^2 \gamma^2[/tex]
stevmg said:I was trying to keep a geometric feel for all this so that when I delve into rapidity I could visualize what I was doing.
Also, why is this matrix referred to as a rotation of axes? What is rotated?
If you look at the diagram below:
You can see that the x' axis has been rotated anticlockwise while the t' axis has been rotated clockwise relative to the x and t axes respectively. The amount of rotation of the axes depends on the relative velocity between the F and F' frames. The relative velocity in the above diagram is 0.6c so the proper time t' =1 translates to t=0.8 and the proper distance x' =1 translates to x=0.8. Note that point P = (x',t') = (0,1) remains on the horizontal hyperbola in the left diagram, for all relative velocities and the point P = (x',t') = 1,0) remains on the vertical hyperbola in the right diagram, for all relative velocities.
Diagrams from http://hubpages.com/hub/Minkowski-Diagram
Last edited:
