Spacetime diagram - Twin paradox

[ghwellsjr]

Jaumzaum's link shows an aborted attempt to combine the last two diagrams from the last post. Here I will show a better way to do this but they still have problems and they cannot show the paths of the message for both twins on the same diagram. First is the combined diagram in which Pam is always at rest and in which she is receiving the messages from Jim. Note that everything she sees is accurate:

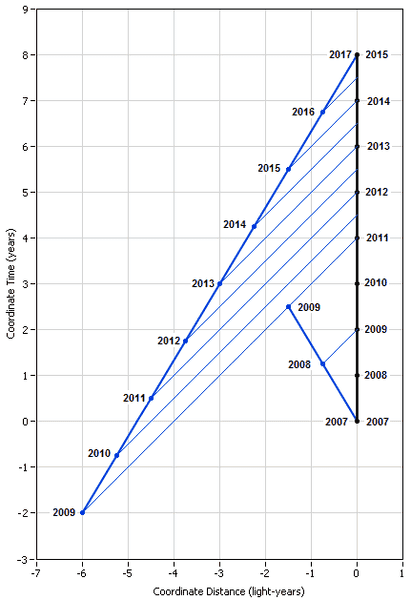
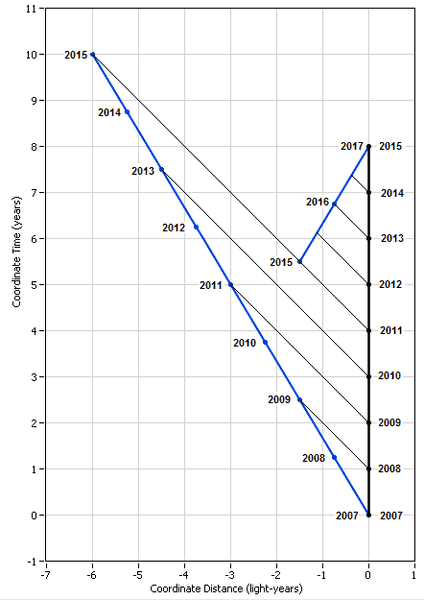
Next is the combined diagram in which Pam is always at rest and in which she is sending messages to Jim. Although it correctly shows when she sent the messages, she cannot tell the path they take to Jim.

This final non-inertial drawing in which Pam is always at rest correctly shows the timings for both Pam and Jim in terms of when they send and receive all the messages:

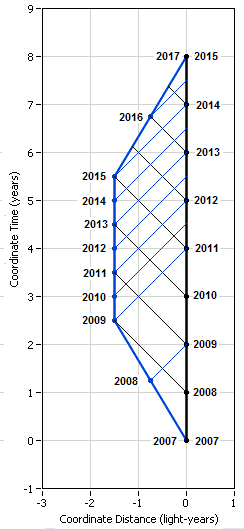
Note that Pam could always use a radar method to determine how far away Jim was and this diagram takes advantage of that information.

 

[PAllen]

Thanks, ghwellsjr, the last is radar coordinates I've referred to, in simplest form (another form is to scale the horizontal - stretching to the left, so the coordinate distance along a horizontal coordinate line corresponds to proper distance along the simultaneity line it represents).

 

[phyti]

Fig. 1 is the typical 'twin' drawing with simultaneity axis, from static twin
Bert's view.
Fig. 2 is traveling twin Bart's view, with distorted space and time
coordinates resulting from simultaneity convention. The 'convention' is a
mathematical device/stipulation and as such cannot relocate events (events
do not move!).
Fig. 3 is fig. 2 without the 'convention' and using relative light speeds.
Fig. 4 is Bart's view with an equivalent G-field as his reversal. Bart will see
Bert curve back toward him as a result of the G-field.


https://www.physicsforums.com/attachment.php?attachmentid=55394&d=1360089535

 

[PAllen]

Fig. 1 is the typical 'twin' drawing with simultaneity axis, from static twin
Bert's view.
Fig. 2 is traveling twin Bart's view, with distorted space and time
coordinates resulting from simultaneity convention. The 'convention' is a
mathematical device/stipulation and as such cannot relocate events (events
do not move!).
Fig. 3 is fig. 2 without the 'convention' and using relative light speeds.
Fig. 4 is Bart's view with an equivalent G-field as his reversal. Bart will see
Bert curve back toward him as a result of the G-field.


https://www.physicsforums.com/attachment.php?attachmentid=55394&d=1360089535

Fig. 4 is ok, but you should be aware that drawn as you have, x coordinated distance is wildly different from proper distance computed along horizontal line in the coordinates. Often, when using some simultaneity convention, you want spatial coordinate differences to reflect proper distances computed on those surfaces. If you do this, the curved path gets highly stretched to the left in your fig. 4.

 

[phyti]

Fig. 4 is ok, but you should be aware that drawn as you have, x coordinated distance is wildly different from proper distance computed along horizontal line in the coordinates. Often, when using some simultaneity convention, you want spatial coordinate differences to reflect proper distances computed on those surfaces. If you do this, the curved path gets highly stretched to the left in your fig. 4.

The stretching/distortion, etc., as in fig. 2, results from the simultaneity convention.
It is is not a deduction using physics, it's, as Einstein states, a definition to assign time and position to the remote reflection events. He also states in a different souce, his definition has nothing to do with physical light propagation. It's to support the pseudo-rest frame that the observer thinks he occupies, with equal light paths out and return, so divide the round trip time in half.
Any locations and times for the reflection events are speculation and inverifiable by the inertially moving observer, until someone can time the light propagation along a 1-way path.

 

[PAllen]

The stretching/distortion, etc., as in fig. 2, results from the simultaneity convention.
It is is not a deduction using physics, it's, as Einstein states, a definition to assign time and position to the remote reflection events. He also states in a different souce, his definition has nothing to do with physical light propagation. It's to support the pseudo-rest frame that the observer thinks he occupies, with equal light paths out and return, so divide the round trip time in half.
Any locations and times for the reflection events are speculation and inverifiable by the inertially moving observer, until someone can time the light propagation along a 1-way path.

You drew a picture in coordinates. I am simply stating a mathematical fact about those coordinates: x coordinate differences are not proportional to proper distance computed along horizontal coordinate lines. There is no requirement that this be so (the metric will contain the scaling, when you transform the metric correctly). However, it is an important feature to know about the coordinates.

Another possible way to get your diagram 4 is if the coordinates are far from orthonormal near the vertical line. This is also ok, as long as you understand its implications. It means that even in the inertial parts of the path, and right near the time axis, the metric will not be close to the Minkowski metric.

 

[phyti]

Fig. 1 shows B accelerating away from A as observed by A.
Fig. 2 shows A accelerating away from B as observed by B.
The curve in fig.2 is a reflection of the curve in fig.1 except fig.2 is scaled down,
due to time dilation and length contraction.
There is no cusp (as shown in post 30) in either curve because the td and lc begin at zero and increase as the speed of B increases. At deceleration, follow the curve backward until B speed equals A speed, with the same results, no cusp. As B decelerates toward A, the G-field points away from A. A cusp at reversal would indicate a repulsive gravitational effect, and occur at minimal relative speed!
A discontinuity is a flag indicating something is not according to physical laws/rules. The instantaneous reversal is such an instance, therefore the results are fiction. In post 38, event A4 in fig.1 does not jump from 16 ly distance to 48 ly in fig.2 unless there is some new and weird undiscovered physics. As stated there, the extreme time and space excursions are math computations using a convention, and not consequences of physical phenomena.
There have been other threads showing that the simplest ‘twin’ case, restricting all acceleration to one twin will appear to be explained by the non inertial asymmetry, but in general cases involving both twins accelerating, the aging question is decided by which twin loses the most time, which is path dependent.

https://www.physicsforums.com/attachments/55914