- #1
71GA
- 208
- 0
Allover the web i am only seeing a statement similar to this:
Well no one out of many writers shows, how to prove this matematically. So this is what interests me here.
First i wanted to know if pair production really cannot happen in vacuum, so i drew a picture and used equations for conservation of energy and conservation of momentum to calculate energy of a photon ##(h \nu)## needed for pair production.
It turns out ##h\nu## is different if i calculate it out of conservation of energy or conservation of momentum. And even more! It can never be the same because equallity would mean parts ##v_1 \cos \alpha## and ##v_2 \cos \beta## should equall speed of light ##c##. Well that cannot happen.
Below is my derivation.
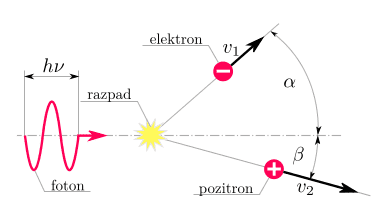
CONSERVATION OF ENERGY:
$$
\scriptsize
\begin{split}
W_{1} &= W_{2}\\
W_f &= W_{e^-} + W_{e^+}\\
h\nu &= W_{ke^-} + W_{0e^-} + W_{ke^+} + W_{0e^+}\\
h\nu &=\left[m_ec^2 \gamma(v_1) - m_ec^2\right] + m_ec^2 + \left[m_ec^2 \gamma(v_2) - m_ec^2\right] + m_ec^2\\
h\nu &=m_ec^2 \gamma(v_1) + m_ec^2 \gamma(v_2)\\
h\nu &=m_ec^2 \left[\gamma(v_1) + \gamma(v_2) \right]\\
\end{split}
$$
CONSERVATION OF MOMENTUM:
##y## direction:
$$
\scriptsize
\begin{split}
p_{1} &= p_{2}\\
0 &= p_{e^-} \sin \alpha - p_{e^+} \sin \beta \\
0 &= m_e v_{1} \gamma(v_{1}) \sin \alpha - m_e v_{2} \gamma(v_{2}) \sin \beta\\
&\text{If $\boxed{\alpha = \beta} \Longrightarrow \boxed{v_1 = v_2}$ and:}\\
0 &= 0
\end{split}
$$
##x## direction:
$$
\scriptsize
\begin{split}
p_{1} &= p_{2}\\
\frac{h}{\lambda} &= p_{e^-} \cos \alpha + p_{e^+} \cos \beta \\
\frac{h \nu}{c} &= m_e v_{1} \gamma(v_{1}) \cos \alpha + m_e v_{2} \gamma(v_{2}) \cos \beta\\
h \nu &= m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big]
\end{split}
$$
Alltogether:
Because momentum in ##y## direction equals 0 (holds for some combinations of ##\alpha, \beta, v_1, v_2##) whole momentum equals just the momentum in ##x## direction. So if i add them i get:
$$
\scriptsize
h \nu = m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big]
$$
From this i can conclude only that i cannot sucessfully apply conservation of energy and conservation of momentum at the same time and therefore pair production in vacuum cannot happen.
QUESTION1:
Why do writers state that 3rd particle is needed so that conservation of momentum holds? What if conservation of momentum holds and conservation of energy doesn't? How can we say which one holds and which one doesnt?
QUESTION2:
Do writters actually mean that if a 3rd particle is included we can achieve ##h \nu## to match in both cases?
QUESTION3:
Can someone show me mathematically how this is done? I mean it should right?
"Pair production is not possible in vaccum, 3rd particle is needed so
that conservation of momentum holds."
that conservation of momentum holds."
Well no one out of many writers shows, how to prove this matematically. So this is what interests me here.
First i wanted to know if pair production really cannot happen in vacuum, so i drew a picture and used equations for conservation of energy and conservation of momentum to calculate energy of a photon ##(h \nu)## needed for pair production.
It turns out ##h\nu## is different if i calculate it out of conservation of energy or conservation of momentum. And even more! It can never be the same because equallity would mean parts ##v_1 \cos \alpha## and ##v_2 \cos \beta## should equall speed of light ##c##. Well that cannot happen.
Below is my derivation.
CONSERVATION OF ENERGY:
$$
\scriptsize
\begin{split}
W_{1} &= W_{2}\\
W_f &= W_{e^-} + W_{e^+}\\
h\nu &= W_{ke^-} + W_{0e^-} + W_{ke^+} + W_{0e^+}\\
h\nu &=\left[m_ec^2 \gamma(v_1) - m_ec^2\right] + m_ec^2 + \left[m_ec^2 \gamma(v_2) - m_ec^2\right] + m_ec^2\\
h\nu &=m_ec^2 \gamma(v_1) + m_ec^2 \gamma(v_2)\\
h\nu &=m_ec^2 \left[\gamma(v_1) + \gamma(v_2) \right]\\
\end{split}
$$
CONSERVATION OF MOMENTUM:
##y## direction:
$$
\scriptsize
\begin{split}
p_{1} &= p_{2}\\
0 &= p_{e^-} \sin \alpha - p_{e^+} \sin \beta \\
0 &= m_e v_{1} \gamma(v_{1}) \sin \alpha - m_e v_{2} \gamma(v_{2}) \sin \beta\\
&\text{If $\boxed{\alpha = \beta} \Longrightarrow \boxed{v_1 = v_2}$ and:}\\
0 &= 0
\end{split}
$$
##x## direction:
$$
\scriptsize
\begin{split}
p_{1} &= p_{2}\\
\frac{h}{\lambda} &= p_{e^-} \cos \alpha + p_{e^+} \cos \beta \\
\frac{h \nu}{c} &= m_e v_{1} \gamma(v_{1}) \cos \alpha + m_e v_{2} \gamma(v_{2}) \cos \beta\\
h \nu &= m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big]
\end{split}
$$
Alltogether:
Because momentum in ##y## direction equals 0 (holds for some combinations of ##\alpha, \beta, v_1, v_2##) whole momentum equals just the momentum in ##x## direction. So if i add them i get:
$$
\scriptsize
h \nu = m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big]
$$
From this i can conclude only that i cannot sucessfully apply conservation of energy and conservation of momentum at the same time and therefore pair production in vacuum cannot happen.
QUESTION1:
Why do writers state that 3rd particle is needed so that conservation of momentum holds? What if conservation of momentum holds and conservation of energy doesn't? How can we say which one holds and which one doesnt?
QUESTION2:
Do writters actually mean that if a 3rd particle is included we can achieve ##h \nu## to match in both cases?
QUESTION3:
Can someone show me mathematically how this is done? I mean it should right?